题目内容
如图,平行四边形的每一个顶点都用直线与两条对边的中点相连.这些直线所围成图形的面积是原平行四边形面积的( )


A.四分之一 B.六分之一 C.八分之一 D.十分之一
B【考点】平行四边形的性质;三角形的面积.
【分析】可先在图形上标记上字母,以便解题,如下图所示,则阴影面积即为四边形PQRS的面积,而四边形PQRS在四边形AEPH中,进而在四边形中通过三角形的面积转化即可得出结论.
【解答】解:如图,
连接平行四边形对边的中点,将这个平行四边形分成四个平行四边形.
注意左上角处的平行四边形AEPH,四边形PQRS就是所求图形在AEPH中的部分.
注意到R是△ADB的两条中线的交点,因此A、R、P三点共线,且AP=3RP,
于是有S△APS=3S△RPS,S△AQP=3S△RQP,
因此SPQRS=
 SPQAS=
SPQAS=
 SAEPH.
SAEPH.
类似的推理可用于其他三个平行四边形,最后得到所需结论为六分之一.
故此题选B.



练习册系列答案
相关题目
根据下表判断方程x2+x﹣3=0的一个根的近似值(精确到0.1)是( )
| x | 1.2 | 1.3 | 1.4 | 1.5 |
| x2+x﹣3 | ﹣0.36 | ﹣0.01 | 0.36 | 0.75 |
A.1.3 B.1.2 C.1.5 D.1.4

 得:
得:
 即
即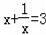
 ,
,




 = 4 ,
= 4 ,
 = 14 ,
= 14 ,
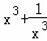
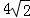 ,则梯形AECD的
,则梯形AECD的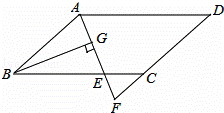



 =0,则第三边长为
=0,则第三边长为 
 B.
B.

 D.
D.


