题目内容
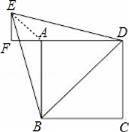
如图,已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F.
(1)找出图中与EF相等的线段,并证明你的结论;
(2)求AF的长.


【考点】正方形的性质;等边三角形的性质;勾股定理.
【分析】(1)连接AE,首先证明△ABE≌△ADE得到∠BEA=30°,再根据题意∠EAF=∠AED+∠ADE=45°,又知EF⊥AD,故可得AF=EF,
(2)设AF=x,由勾股定理得EF2+FD2=ED2,列出等量关系式,解得x.
【解答】解:(1)AF=EF;
理由如下:连接AE,
∵△DBE是正三角形,
∴EB=ED.
∵AD=AB,AE=AE,
∴△ABE≌△ADE.
∴∠BEA=∠DEA=
 ×60°=30°.
×60°=30°.
∵∠EDA=∠EDB﹣∠ADB=60°﹣45°=15°,
∴∠EAF=∠AED+∠ADE=45°.
∵EF⊥AD,
∴△EFA是等腰直角三角形.
∴EF=AF.
(2)设AF=x,
∵AD=2,BD=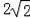
 =ED,FD=2+x,
=ED,FD=2+x,
在Rt△EFD中,
由勾股定理得EF2+FD2=ED2即x2+(2+x)2=(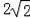
 )2
)2
∴x=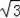
 ﹣1(x=﹣
﹣1(x=﹣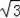
 ﹣1舍去),∴AF=
﹣1舍去),∴AF=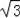
 ﹣1.
﹣1.


一个不透明的盒中装有若干个只有颜色不同的红球与白球.
(1)若盒中有2个红球和2个白球,从中任意摸出两个球恰好是一红一白的概率是多少?请用画树状图或列表的方式说明;
(2)若先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:每次摸球前先搅拌均匀,摸出一个球,记录颜色后放回盒中,再继续,一共做了50次,统计结果如下表:
| 球的颜色 | 无记号 | 有记号 | ||
| 红色 | 白色 | 红色 | 白色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球实验的结果可估算盒中红球、白球各占总球数的百分之几?
(3)在(2)的条件下估算盒中红球的个数.
 用含x的代数式表示y为( )
用含x的代数式表示y为( ) B、
B、 C、
C、 D、
D、
 +
+ )2﹣(
)2﹣(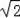







 的图象上,过点A的直线y=x+b交反比例函数y=
的图象上,过点A的直线y=x+b交反比例函数y=
