题目内容
已知直角三角形的两边长为x，y，且满足|x2﹣4|+
=0，则第三边长为
2
，
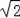
或
．
【考点】勾股定理；二次根式的性质与化简．
【分析】首先利用绝对值以及算术平方根的性质得出x，y的值，再利用分类讨论结合勾股定理求出第三边长．
【解答】解：∵x、y为直角三角形的两边的长，满足|x2﹣4|+=0，
∴x2﹣4=0，y2﹣5y+6=0，
解得：x1=2，x2=﹣2（不合题意舍去），y1=2，y2=3，
当直角边长为：2，2，则第三边长为：2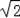
，
当直角边长为：2，3，则第三边长为：
，
当直角边长为2，斜边长为3，则第三边长为：
．
故答案为：2
，或
．
练习册系列答案
相关题目
一个不透明的盒中装有若干个只有颜色不同的红球与白球．
（1）若盒中有2个红球和2个白球，从中任意摸出两个球恰好是一红一白的概率是多少？请用画树状图或列表的方式说明；
（2）若先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验．摸球实验的要求：每次摸球前先搅拌均匀，摸出一个球，记录颜色后放回盒中，再继续，一共做了50次，统计结果如下表：
| 球的颜色 | 无记号 | 有记号 | ||
| 红色 | 白色 | 红色 | 白色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球实验的结果可估算盒中红球、白球各占总球数的百分之几？
（3）在（2）的条件下估算盒中红球的个数．
]=3，求满足条件的所有正整数x．
﹣
