题目内容
4.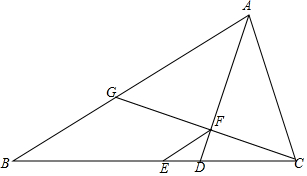 如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.
如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.
分析 先根据E为BC的中点,EF∥AB,得到F是CG的中点,再延长AF至P,使得PF=AF,根据SAS判定△PFC≌△AFG,进而得出AG=CP,∠GAF=∠P,再根据AD是△ABC的平分线,得到∠CAF=∠GAF=∠P,得出AC=CP,即可得到AG=AC.
解答 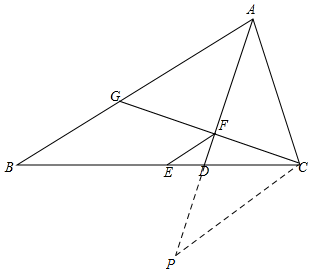 证明:∵E为BC的中点,EF∥AB,
证明:∵E为BC的中点,EF∥AB,
∴$\frac{CF}{FG}$=$\frac{CE}{EB}$=1,
∴F是CG的中点,即CF=GF,
如图,延长AF至P,使得PF=AF,
在△PFC和△AFG中,
$\left\{\begin{array}{l}{PF=AF}\\{∠PFC=∠AFG}\\{CF=GF}\end{array}\right.$,
∴△PFC≌△AFG(SAS),
∴AG=CP,∠GAF=∠P,
又∵AD是△ABC的平分线,
∴∠CAF=∠GAF,
∴∠P=∠CAF,
∴AC=CP,
∴AG=AC.
点评 本题主要考查了三角形中位线定理,角平分线的定义以及全等三角形的判定与性质,解决问题的关键是作辅助线构造全等三角形,依据全等三角形的对应边相等,对应角相等进行推导.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.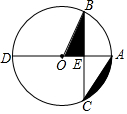 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )| A. | $\frac{8}{9}π-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{8}{9}π-\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{18}π-\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{16}{9}π-\frac{{2\sqrt{3}}}{3}$ |
16. 如图,已知∠1=85°,∠2=95°,∠4=125°,则∠3的度数为( )
如图,已知∠1=85°,∠2=95°,∠4=125°,则∠3的度数为( )
 如图,已知∠1=85°,∠2=95°,∠4=125°,则∠3的度数为( )
如图,已知∠1=85°,∠2=95°,∠4=125°,则∠3的度数为( )| A. | 95° | B. | 85° | C. | 70° | D. | 125° |
13.小芳和小丽是乒乓球运动员,在一次比赛中,每人只允许保“双打”或“单打”中的一项,那么两人同时报单打的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
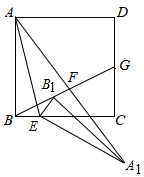 如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1; 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.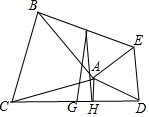 如图,△ABC,△ADE为等边三角形,F、G分别是BE、CD的中点,AH是△ACD的高,求证:FG=FH.
如图,△ABC,△ADE为等边三角形,F、G分别是BE、CD的中点,AH是△ACD的高,求证:FG=FH.