题目内容
19.已知a及b均为正整数,其中a>b.(a)因式分解ab+a+2b+2.
(b)若ab+a+2b=49,则a及b是否同为奇数.
分析 (a)根据分组分解法即可求出答案.
(b)先将ab+a+2b=49化为(b+1)(a+2)=3×17,然后分情况进行讨论即可得出答案.
解答 解:(a)ab+a+2b+2=(ab+a)+(2b+2)=a(b+1)+2(b+1)=(b+1)(a+2).
(b)若ab+a+2b=49,
∴a(b+1)+2(b+1)=51
∴(b+1)(a+2)=51,
∴(b+1)(a+2)=3×17,
当b+1=3,a+2=15时,
此时b=2,a=13,
当b+1=15,a+2=3,
此时b=14,a=1
所以a及b不能同为奇数
点评 本题考查因式分解法,解题的关键是熟练运用分组分解法,本题属于基础题型.

练习册系列答案
相关题目
9.如果关于x的不等式(a+5)x>a+5的解集为x<1那么,a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-5 | D. | a<-5 |
7.在不等式$\frac{2}{3}$x+2>x的解集中,正整数解的个数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.下列说法中,正确的是( )
| A. | 对角线互相平分的四边形是矩形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线垂直的四边形是菱形 | |
| D. | 对角线垂直平分且相等的四边形是正方形 |
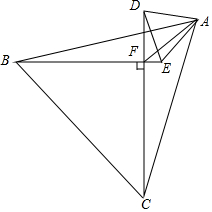 正△ABC,正△ADE,BE⊥CD,F为垂足,AF=1,求S△ABC+S△ADE.
正△ABC,正△ADE,BE⊥CD,F为垂足,AF=1,求S△ABC+S△ADE.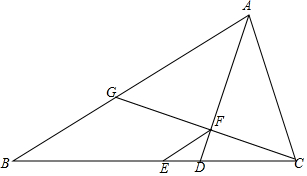 如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.
如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC. 图中,l1∥l2∥l3,若EF=14cm,求DE.
图中,l1∥l2∥l3,若EF=14cm,求DE.


