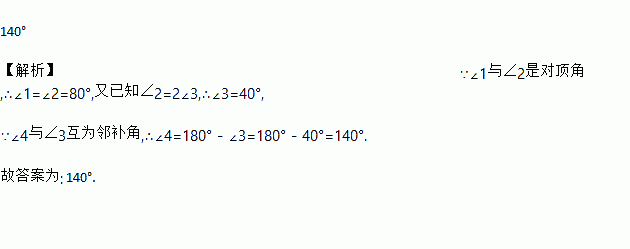题目内容
如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=__________.
 140°
【解析】∵∠1与∠2是对顶角,∴∠1=∠2=80°,又已知∠2=2∠3,∴∠3=40°,
∵∠4与∠3互为邻补角,∴∠4=180°-∠3=180°-40°=140°.
故答案为: 140°.
140°
【解析】∵∠1与∠2是对顶角,∴∠1=∠2=80°,又已知∠2=2∠3,∴∠3=40°,
∵∠4与∠3互为邻补角,∴∠4=180°-∠3=180°-40°=140°.
故答案为: 140°.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
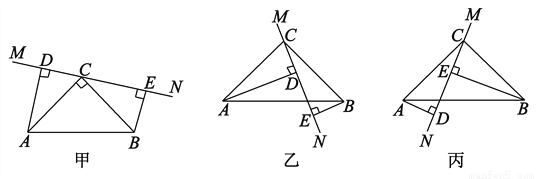
(1)当直线MN绕点C旋转到图甲的位置时,试说明:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,试说明:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
 (1)证明见解析;()证明见解析;(3)AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等)理由见解析.
【解析】试题分析:(1)由∠ACB=90°,得∠BCE+∠ACD=90°,而AD⊥MN于D,BE⊥MN于E.则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE.,易得
Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE...
(1)证明见解析;()证明见解析;(3)AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等)理由见解析.
【解析】试题分析:(1)由∠ACB=90°,得∠BCE+∠ACD=90°,而AD⊥MN于D,BE⊥MN于E.则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE.,易得
Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE... 不等式的解集在数轴上表示如图所示,则该不等式可能是___________________.

 不唯一,如x-1≤0
【解析】由图形可知,不等式的解集为x≤1.只要所写的不等式的解集为x≤1,即可,答案不唯一.
不唯一,如x-1≤0
【解析】由图形可知,不等式的解集为x≤1.只要所写的不等式的解集为x≤1,即可,答案不唯一. 根据下列已知条件,能唯一画出△ABC的是( )
A. ∠A=36°,∠B=45°,AB=4 B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,CA=1 D. ∠C=90°,AB=6
 A
【解析】A. ∠A=36°,∠B=45°,AB=4,利用原理“ASA”可以画出唯一的三角形;B、C、D都不能唯一的作出三角形.故选A.
A
【解析】A. ∠A=36°,∠B=45°,AB=4,利用原理“ASA”可以画出唯一的三角形;B、C、D都不能唯一的作出三角形.故选A. 探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
 (1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
【解析】(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:(1)1,3,(2)1,6,(3)1, , ,.
(1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
【解析】(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:(1)1,3,(2)1,6,(3)1, , ,. 在括号内填写依据:
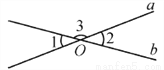
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°(____________________),
∠1=∠2(____________________).
 邻补角互补@对顶角相等
【解析】因为∠1和∠3是邻补角,∠1+∠3=180°, 因为∠1和∠2是对顶角,∠1=∠2,
故答案为: 邻补角互补,对顶角相等.
邻补角互补@对顶角相等
【解析】因为∠1和∠3是邻补角,∠1+∠3=180°, 因为∠1和∠2是对顶角,∠1=∠2,
故答案为: 邻补角互补,对顶角相等. 如图,直线AB和CD相交于点O,则∠AOC的对顶角是__________.
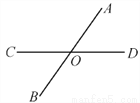
 ∠BOD
【解析】因为AB和CD交于点O,则∠AOC的对顶角是∠BOC,故答案为:∠BOC.
∠BOD
【解析】因为AB和CD交于点O,则∠AOC的对顶角是∠BOC,故答案为:∠BOC. 用计算器求下列格式的值(结果精确到0.0001).
(1)tan63°27′;
(2)cos18°59′27″;
(3)sin67°38′24″.
 (1)2.0013;(2)0.9456;(3)0.9248.
【解析】试题分析:将度、分、秒统一为度,然后利用计算器即可求出结果.
试题解析:
【解析】
(1)tan63°27′=tan63.45°≈2.0013;
(2)cos18°59′27″=cos18.9908°≈0.9456;
(3)sin67°38′24″=sin67.64°≈0.9248.
(1)2.0013;(2)0.9456;(3)0.9248.
【解析】试题分析:将度、分、秒统一为度,然后利用计算器即可求出结果.
试题解析:
【解析】
(1)tan63°27′=tan63.45°≈2.0013;
(2)cos18°59′27″=cos18.9908°≈0.9456;
(3)sin67°38′24″=sin67.64°≈0.9248. 一个不透明的袋中共有20个球,它们除颜色不同外,其余均相同,其中8个白球,5个黄球,5个绿球,2个红球,则任意摸出一个球是红球的概率是( )
A.  B.
B. 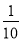 C.
C. 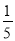 D.
D. 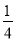
 B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B.
B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B.