题目内容
7.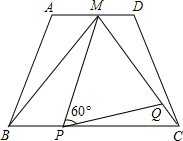 如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.
如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.(1)求证:AB=CD;
(2)动点P,Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变,设PC=x,MQ=y,求y与x之间的函数关系;
(3)在(2)中当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两点为顶点的四边形是平行四边形?
分析 (1)先根据SAS得出△AMB与△DMC全等,再利用全等三角形的性质求出AB=DC;
(2)先根据相似三角形的判定得出△BMP与△CPQ相似,再利用相似三角形的性质列出方程求出关系式.
(3)根据平行四边形分情况讨论即可.
解答 (1)证明:∵△MBC是等边三角形,
∴MB=MC,∠MBC=∠MCB=60°,
∵M是AD中点,
∴AM=MD,
∵AD∥BC,
∴∠AMB=∠MBC=60°,∠DMC=∠MCB=60°.
∴△AMB≌△DMC,
∴AB=DC;
(2)在等边三角形MBC中,MB=MC=BC=4,∠MBC=∠MCB=60°,∠MPQ=60°,
∴∠BMP+∠BPM=∠BPM+∠QPC=120°,
∴∠BMP=∠QPC,
∴△BMP∽△CPQ,
∴$\frac{PC}{BM}=\frac{CQ}{BP}$,
令PC=x,MQ=y,则BP=4-x,QC=4-y,
∴$\frac{x}{4}=\frac{4-y}{4-x}$,
∴y=$\frac{1}{4}$x2-x+4=$\frac{1}{4}$(x-2)2+3;
(3)当BP=1时,有BP平行且等于AM,BP平行且等于MD,则四边形ABPM四边形MBPD均为平行四边形.
当BP=3时,又PC平行且等于AM,PC平行且等于MD,
则四边形MPCD和四边形APCM均为平行四边形.
∴当BP=1或BP=3时,以点P、M和A、B、C、D中的两个点为顶点的四边形是平行四边形.
点评 此题主要考查三角形的全等相似性质以及平行四边形的判定,关键全等三角形的判定和根据相似三角形性质得出关系式.

练习册系列答案
相关题目
15.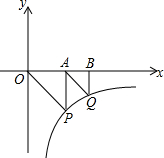 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )| A. | (6,0) | B. | (9,0) | C. | ($\frac{3+3\sqrt{5}}{2}$,0) | D. | ($\frac{3\sqrt{2}+3}{2}$,0) |
13.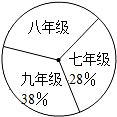 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )| 图书种类 | 频数 | 频率 |
| 科普知识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其它 | 144 | 0.06 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
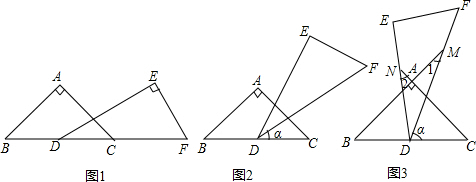
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放在平面直角坐标系中,
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放在平面直角坐标系中,