题目内容
15.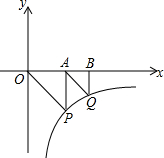 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )| A. | (6,0) | B. | (9,0) | C. | ($\frac{3+3\sqrt{5}}{2}$,0) | D. | ($\frac{3\sqrt{2}+3}{2}$,0) |
分析 利用反比例函数图象上点的坐标性质求出P点坐标,进而表示出Q点坐标,进而得出答案.
解答 解:设P点的坐标为:(x,-x),则-x2=-9,
解得:x=±3(负数舍去),
故P(3,-3),
设Q(3+a,-a),
则-a(3+a)=-9,
解得:a1=-$\frac{3+3\sqrt{5}}{2}$(不合题意舍去),a2=$\frac{-3+3\sqrt{5}}{2}$,
则3+$\frac{-3+3\sqrt{5}}{2}$=$\frac{3+3\sqrt{5}}{2}$,
故点B的坐标为:($\frac{3+3\sqrt{5}}{2}$,0).
故选:C.
点评 此题主要考查了反比例函数图象上点的坐标性质,得出P点坐标是解题关键.

练习册系列答案
相关题目
10.|5|的值是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |
5.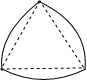 如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
 如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )| A. | 50π-50$\sqrt{3}$ | B. | 50π-25$\sqrt{3}$ | C. | 25π+50$\sqrt{3}$ | D. | 50π |
6.函数y=mxm-1+(m-1)是一次函数,则m值( )
| A. | m≠0 | B. | m=2 | C. | m=2或4 | D. | m>2 |
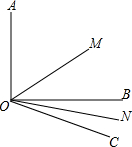 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC; 如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD. 如图,已知平面内A、B、C三点.
如图,已知平面内A、B、C三点.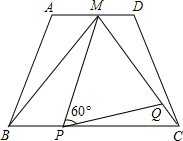 如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.
如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.