题目内容
17.解分式方程:$\frac{3+x}{3-x}$+$\frac{36}{{x}^{2}-9}$=-1.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:-x2-6x-9+36=-x2+9,
移项合并得:6x=18,
解得:x=3,
经检验x=3是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.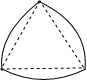 如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
 如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )| A. | 50π-50$\sqrt{3}$ | B. | 50π-25$\sqrt{3}$ | C. | 25π+50$\sqrt{3}$ | D. | 50π |
2.如图,在圆形纸片和三角形纸片中都刚好能裁剪出棱长为acm的正方体纸盒的表面,那么两种纸片的利用率(纸片利用率=$\frac{纸片被利用的面积}{纸片的总面积}$×100%)的大小关系为( )
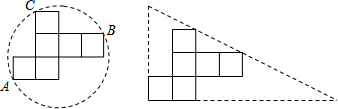

| A. | 圆形纸片利用率大 | B. | 三角形纸片利用率大 | ||
| C. | 两种纸片的利用率一样 | D. | 利用率与a的值有关,无法判断 |
6.函数y=mxm-1+(m-1)是一次函数,则m值( )
| A. | m≠0 | B. | m=2 | C. | m=2或4 | D. | m>2 |
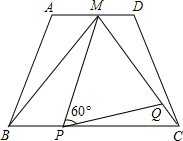 如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.
如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.