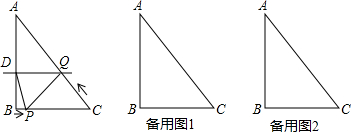
题目内容
2.如图1,含30°角的直角三角板DEF(∠EDF=30°)与含45°角的直角三角板的斜边在同一直线上,D为BC的中点,将直角三角板DEF绕点D按逆时针方向旋转∠α(0°<α<180°),在旋转过程中:(1)如图2,当∠α=15°时,DE∥AB;当∠α=105°时,DE⊥AB;
(2)如图3,当直角三角板DEF的边DF、DE分别交BA、CA的延长线于点M、N时:
①∠1与∠2度数的和是否变化?若不变,求出∠1与∠2度数的和;若变化,请说明理由;
②若使得∠1=2∠2,求出∠1、∠2的度数,并直接写出此时∠α的度数;
③若使得∠1≥$\frac{2}{3}$∠2,求∠α的度数范围.
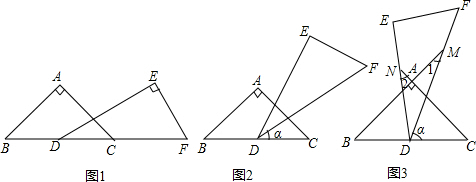
分析 (1)当∠EDC=∠B=45°时,DE∥AB,根据平行线的性质得30°+α=45°,解得α=15°;当DE∥AC时,DE⊥AB,根据平行线的性质得30°+α+45°=180°,解得α=105°;
(2)①连结MN,如图3,在△AMN中,由三角形内角和定理得∠ANM+∠AMN+∠MAN=180°,则∠ANM+∠AMN=90°,再在△MND中,利用三角形内角和定理得到∠2+∠ANM+∠AMN+∠1+∠MDN=180°,所以∠1+∠2=60°;
②根据∠1与∠2的关系列方程组$\left\{\begin{array}{l}{∠1+∠2=60°}\\{∠1=2∠2}\end{array}\right.$,然后解方程组即可;再根据三角形内角和定理和对顶角相等得到∠C+∠MDC=∠1+∠MAC,即45°+α=40°+90°,解得α=85°;
③由∠1≥$\frac{2}{3}$∠2,∠1+∠2=60°可解得∠1≥24°,由于∠C+∠MDC=∠1+∠MAC,即45°+α=∠1+90°,则∠1=α-45°,所以α-45°≥24°,解得α≥69°,利用直角三角板DEF的边DF、DE分别交BA、CA的延长线于点M、N得到α<90°,于是得到69°≤α<90°.
解答 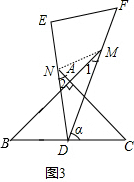 解:(1)∵∠B=45°,
解:(1)∵∠B=45°,
∴当∠EDC=∠B=45°时,DE∥AB,
而∠EDF=30°,
∴30°+α=45°,解得α=15°;
当DE∥AC时,DE⊥AB,
此时∠C+∠EDC=180°,
∴30°+α+45°=180°,解得α=105°;
故答案为15°,105°;
(2)①∠1与∠2度数的和不变.
连结MN,如图3,
在△AMN中,∵∠ANM+∠AMN+∠MAN=180°,
∴∠ANM+∠AMN=90°,
在△MND中,∵∠DNM+∠DMN+∠MDN=180°,
即∠2+∠ANM+∠AMN+∠1+∠MDN=180°,
∴∠1+∠2=180°-90°-30°=60°;
②根据题意得$\left\{\begin{array}{l}{∠1+∠2=60°}\\{∠1=2∠2}\end{array}\right.$,解得$\left\{\begin{array}{l}{∠1=40°}\\{∠2=20°}\end{array}\right.$;
∵∠C+∠MDC=∠1+∠MAC,
即45°+α=40°+90°,
∴α=85°;
③∵∠1≥$\frac{2}{3}$∠2,∠1+∠2=60°,
∴∠1≥$\frac{2}{3}$(60°-∠1),
∴∠1≥24°,
∵∠C+∠MDC=∠1+∠MAC,
即45°+α=∠1+90°,
∴∠1=α-45°,
∴α-45°≥24°,解得α≥69°,
∴∠α的度数范围为69°≤α<90°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.也考查了解二元一次方程组.合理选择三角形后利用三角形内角和定理列等量关系是解决问题的关键,同时运用不等式的性质解决∠α的度数范围.

 阅读快车系列答案
阅读快车系列答案| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |
 如图,△ABC中,DE是边AB的垂直平分线,AD=9,BC=11,AB=14,则BD的长是( )
如图,△ABC中,DE是边AB的垂直平分线,AD=9,BC=11,AB=14,则BD的长是( )| A. | 9 | B. | 11 | C. | 14 | D. | 无法确定 |
| A. | -3x3y2z的系数是3 | B. | x2+x3是5次多项式 | ||
| C. | $\frac{1}{{x}^{2}}$不是整式 | D. | πr2是3次单项式 |
 如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.
如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形. 如图所示,在四边形ABCD中,AB∥CD,AB=CD=BC,求证:四边形ABCD是菱形.
如图所示,在四边形ABCD中,AB∥CD,AB=CD=BC,求证:四边形ABCD是菱形.