题目内容
18.如图,把两张大小和形状相同的长方形纸片沿对角线剪开,得到四个大小和形状相同的直角三角形,两直角边分别是a,b,斜边长为c(c>a>b),把这四个直角三角形围成如图的大小两个正方形.
(1)图中的小正方形面积=(a-b)2;
(2)图中的大正方形的面积是c2或a2+b2;
(3)若a=2,b=1,试求大正方形的面积.
分析 (1)根据正方形的面积公式即可得到结论;
(2)根据正方形的面积公式即可得到结论;
(3)根据勾股定理求得正方形的边长,然后由正方形的面积公式即可得到结果.
解答 解:(1)图中的小正方形面积=(a-b)2;
故答案为:(a-b)2;
(2)图中的大正方形的面积=c2,或图中的大正方形的面积=4×$\frac{1}{2}×$ab+(a-b)2=a2+b2;
故答案为:c2或a2+b2;
(3)∵c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴大正方形的面积=($\sqrt{5}$)2=5.
点评 本题考查了勾股定理的证明,三角形面积的求法,正方形的面积,正确的识图是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
15.下列说法正确的是( )
| A. | 近似数25.0与25精确的度相同 | B. | 0.3998精确到百分位约等于0.4 | ||
| C. | 近似数0.003020(精确到万分位) | D. | 0.050(精确到千分位) |
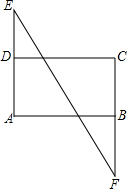 如图,已知∠E=∠F,∠A=∠C,探求AB与CD的位置关系,并说明理由.
如图,已知∠E=∠F,∠A=∠C,探求AB与CD的位置关系,并说明理由.
 已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.
已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.
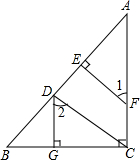 如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.
如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.