题目内容
1. 如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE、BD、CE相交于点F,且∠ADB=∠BAC.求证:四边形ABFE为菱形.
如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE、BD、CE相交于点F,且∠ADB=∠BAC.求证:四边形ABFE为菱形.
分析 由旋转的性质得出AD=AB,AE=AC,∠DAE=∠BAC,得出∠ABD=∠ADB,∠ACE=∠AEC,∠BAD=∠CAE,证出∠DAE=∠ADB,得出AE∥BD,由三角形内角和定理证出∠ABD=∠ACE,得出∠BAC=∠ACE,证出AB∥CE,得出四边形ABFE是平行四边形,即可得出结论.
解答 证明:由旋转的性质得:△ADE≌△ABC,
∴AD=AB,AE=AC,∠DAE=∠BAC,
∴∠ABD=∠ADB,∠ACE=∠AEC,∠BAD=∠CAE,
∵∠ADB=∠BAC,
∴∠DAE=∠ADB,
∴AE∥BD,
∵∠BAD+∠ABD+∠ADB=180°,∠CAE+∠ACE+∠AEC=180°,
∴∠ABD=∠ACE,
∴∠BAC=∠ACE,
∴AB∥CE,
∴四边形ABFE是平行四边形,
又∵AB=AE,
∴四边形ABFE为菱形.
点评 本题考查了旋转的性质、平行四边形的判定方法、菱形的判定方法、等腰三角形的性质、平行线的判定方法;熟练掌握旋转的性质,证明四边形是平行四边形是解决问题的关键,有一定难度.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
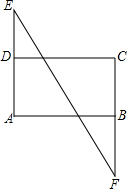 如图,已知∠E=∠F,∠A=∠C,探求AB与CD的位置关系,并说明理由.
如图,已知∠E=∠F,∠A=∠C,探求AB与CD的位置关系,并说明理由. 如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推.
如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推.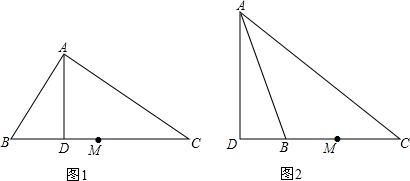
 已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.
已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.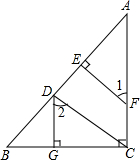 如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.
如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.