题目内容
15. 如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )| A. | 56° | B. | 66° | C. | 24° | D. | 34° |
分析 先根据平行线的性质,得出∠CEH=124°,再根据CD⊥EF,即可得出∠2的度数.
解答  解:∵AB∥CD,∠1=124°,
解:∵AB∥CD,∠1=124°,
∴∠CEH=124°,
∴∠CEG=56°,
又∵CD⊥EF,
∴∠2=90°-∠CEG=34°.
故选:D.
点评 本题主要考查了平行线的性质与垂线的定义,解题时注意:两直线平行,同位角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列各式错误的是( )
| A. | -4>-5 | B. | -(-3)=3 | C. | -|-4|=4 | D. | 16÷(-4)2=1 |
7.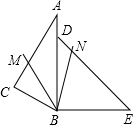 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
4. 如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
 如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )| A. | 8 | B. | 8π | C. | 20 | D. | 20π |
5.已知2a=3b,则$\frac{a}{b}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
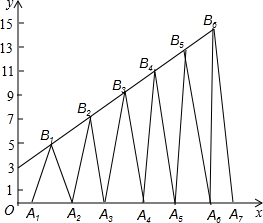 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a. 如图,矩形ABCD中,E是BC上一点,且$\frac{BE}{EC}$=4,AE⊥DE,求$\frac{AB}{BC}$的值.
如图,矩形ABCD中,E是BC上一点,且$\frac{BE}{EC}$=4,AE⊥DE,求$\frac{AB}{BC}$的值. 已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离.
已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离. 如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.
如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.