题目内容
如图,在正方形ABCD中,对角线的交点为O,点E是BC延长线上一点,CF⊥DE交DE于F,交AB于G,
(1)求证:△DCE≌△CBG.
(2)EO与OG垂直吗?请说明理由.
(3)张聪同学在研究这道几何题时,他猜想当E点沿直线CB向B点运动而其余条件不变时,(1)(2)问的结论仍然成立.请帮助张聪同学画出当E点运动到线段上而其余条件不变时的图形,并标上字母.你认为他的猜想对吗?(简要说明理由)
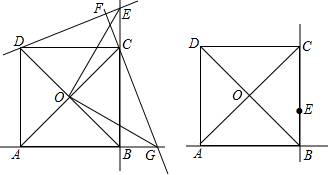
(1)求证:△DCE≌△CBG.
(2)EO与OG垂直吗?请说明理由.
(3)张聪同学在研究这道几何题时,他猜想当E点沿直线CB向B点运动而其余条件不变时,(1)(2)问的结论仍然成立.请帮助张聪同学画出当E点运动到线段上而其余条件不变时的图形,并标上字母.你认为他的猜想对吗?(简要说明理由)

考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)根据正方形的性质可得BC=CD,再根据同角的余角相等求出∠CDE=∠BCG,然后利用“角边角”证明△DCE和△CBG全等即可;
(2)根据全等三角形对应边相等可得BG=CE,再利用“边角边”证明△BOG和△COE全等,根据全等三角形对应角相等可得∠BOG=∠COE,从而求出∠EOG=∠BOC,再根据正方形的对角线互相垂直证明即可;
(3)证明方法与(1)(2)完全相同.
(2)根据全等三角形对应边相等可得BG=CE,再利用“边角边”证明△BOG和△COE全等,根据全等三角形对应角相等可得∠BOG=∠COE,从而求出∠EOG=∠BOC,再根据正方形的对角线互相垂直证明即可;
(3)证明方法与(1)(2)完全相同.
解答:(1)证明:在正方形ABCD中,BC=CD,
∵CF⊥DE,
∴∠CDE+∠DCF=90°,
∵∠DCF+∠BCG=180°-90°=90°,
∴∠CDE=∠BCG,
在△DCE和△CBG中,
,
∴△DCE≌△CBG(ASA);
(2)解:∵△DCE≌△CBG,
∴BG=CE,
∵四边形ABCD是正方形,
∴∠ABO=∠BCO=45°,OB=OC,
∴∠OBG=∠OCE=135°,
在△BOG和△COE中,
,
∴△BOG≌△COE(SAS),
∴∠BOG=∠COE,
∴∠EOG=∠BOC=90°,
∴EO⊥OG;
(3)解:结论仍然成立.
理由如下:如图,同(1)可证△DCE≌△CBG,
同(2)可证△BOG≌△COE,
∴∠BOG=∠COE,
∴∠EOG=∠BOC=90°,
∴EO⊥OG.
∵CF⊥DE,
∴∠CDE+∠DCF=90°,
∵∠DCF+∠BCG=180°-90°=90°,
∴∠CDE=∠BCG,
在△DCE和△CBG中,
|
∴△DCE≌△CBG(ASA);
(2)解:∵△DCE≌△CBG,

∴BG=CE,
∵四边形ABCD是正方形,
∴∠ABO=∠BCO=45°,OB=OC,
∴∠OBG=∠OCE=135°,
在△BOG和△COE中,
|
∴△BOG≌△COE(SAS),
∴∠BOG=∠COE,
∴∠EOG=∠BOC=90°,
∴EO⊥OG;
(3)解:结论仍然成立.
理由如下:如图,同(1)可证△DCE≌△CBG,
同(2)可证△BOG≌△COE,
∴∠BOG=∠COE,
∴∠EOG=∠BOC=90°,
∴EO⊥OG.
点评:本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并确定出三角形全等的条件是解题的关键,难点在于(2)也要证明三角形全等.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
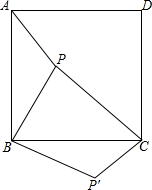 如图,四边形ABCD为正方形,△ABP≌△CBP′,∠PBP′=90°,若PA2+PC2=2PB2.证明:P在对角线AC上.
如图,四边形ABCD为正方形,△ABP≌△CBP′,∠PBP′=90°,若PA2+PC2=2PB2.证明:P在对角线AC上. 直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n|-
直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n|-