题目内容
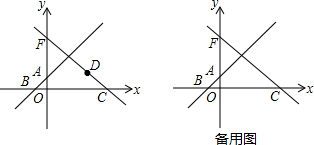 在平面直角坐标系xOy中,直线AB与直线y=-
在平面直角坐标系xOy中,直线AB与直线y=-| 3 |
| 4 |
(1)求直线AB的解析式和点D横坐标的取值范围;
(2)当△CBD为直角三角形时,求BD的长;
(3)当△CBD为等腰直角三角形时,求点D的坐标.
考点:一次函数综合题
专题:
分析:(1)设直线AB的解析式为y=kx+b,将B(-1,0),A(0,1)代入,利用待定系数法即可求出直线AB的解析式;根据点D是射线FC上的一个动点及F点横坐标为0,即可求出点D横坐标的取值范围;
(2)先由直线y=-
x+3交x轴于点C,求出C点坐标为(4,0).根据点D是射线FC上的一个动点及B(-1,0),可知当△CBD为直角三角形时,只能∠BDC=90°,设D(x,-
x+3).在△CBD中根据勾股定理列出方程(x+1)2+(-
x+3)2+(x-4)2+(-
x+3)2=52,解方程求出x的值,再代入两点间的距离公式,计算即可求出BD的长;
(3)由(2)可知,满足△CBD为直角三角形的D点只有一个,求出此时CD的长度,与BD进行比较,如果相等,(2)中所求D点坐标即为所求;如果不相等,那么满足条件的D点不存在.
(2)先由直线y=-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
(3)由(2)可知,满足△CBD为直角三角形的D点只有一个,求出此时CD的长度,与BD进行比较,如果相等,(2)中所求D点坐标即为所求;如果不相等,那么满足条件的D点不存在.
解答:解:(1)设直线AB的解析式为:y=kx+b,
∵B(-1,0),A(0,1),
∴
,
解得:
,
∴直线AB的解析式为:y=x+1,
∵点D是射线FC上的一个动点,
∴点D横坐标的取值范围为:x>0;
(2)∵直线y=-
x+3交x轴于点C,
∴0=-
x+3,
解得:x=4,
∴点C(4,0),
当△CBD为直角三角形时,只能∠BDC=90°,设D(x,-
x+3).
∵∠BDC=90°,
∴BD2+CD2=BC2,
即(x+1)2+(-
x+3)2+(x-4)2+(-
x+3)2=52,
整理得5x2-24x+16=0,
解得x1=
,x2=4(不合题意舍去),
∴D(
,
).
∵BD2=(
+1)2+(
)2=9,
∴BD=3;
(3)由(2)可知,满足△CBD为直角三角形的D点只有一个,此时D(
,
),BD=3,
∵CD=
=4,
∴BD≠CD,
∴满足△CBD为等腰直角三角形的D点不存在.
∵B(-1,0),A(0,1),
∴
|
解得:
|
∴直线AB的解析式为:y=x+1,
∵点D是射线FC上的一个动点,
∴点D横坐标的取值范围为:x>0;
(2)∵直线y=-
| 3 |
| 4 |
∴0=-
| 3 |
| 4 |
解得:x=4,
∴点C(4,0),
当△CBD为直角三角形时,只能∠BDC=90°,设D(x,-
| 3 |
| 4 |
∵∠BDC=90°,
∴BD2+CD2=BC2,
即(x+1)2+(-
| 3 |
| 4 |
| 3 |
| 4 |
整理得5x2-24x+16=0,
解得x1=
| 4 |
| 5 |
∴D(
| 4 |
| 5 |
| 12 |
| 5 |
∵BD2=(
| 4 |
| 5 |
| 12 |
| 5 |
∴BD=3;
(3)由(2)可知,满足△CBD为直角三角形的D点只有一个,此时D(
| 4 |
| 5 |
| 12 |
| 5 |
∵CD=
(
|
∴BD≠CD,
∴满足△CBD为等腰直角三角形的D点不存在.
点评:本题是一次函数的综合题,其中涉及到运用待定系数法求直线的解析式,一次函数图象上点的坐标特征,勾股定理与等腰直角三角形的性质,难度适中.

练习册系列答案
相关题目
下列变形正确的是( )
| A、若x2=y2,则x=y | ||||
B、若
| ||||
| C、若x(x-2)=3(x-2),则x=3 | ||||
| D、若(m+n)x=(m+n)y,则x=y, |
 已知抛物线y=-x2+2x+m-2与y轴交于点A(0,2m-7),与直线y=2x交于点B,C(B在C的右侧).求抛物线的解析式.
已知抛物线y=-x2+2x+m-2与y轴交于点A(0,2m-7),与直线y=2x交于点B,C(B在C的右侧).求抛物线的解析式.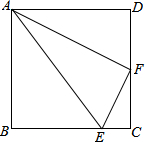 设点E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,BE=3EC,F为CD的中点,连结AF,AE,EF.问△AEF是什么形状的三角形?请说明理由.
设点E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,BE=3EC,F为CD的中点,连结AF,AE,EF.问△AEF是什么形状的三角形?请说明理由.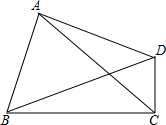 如图,在四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BCD.若BC=7,AC=4
如图,在四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BCD.若BC=7,AC=4