题目内容
9．已知点A（x1，y1），B（x2，y2）是反比例函数y=$\frac{k}{x}$（k＞0）图象上的两点，若x1＜0＜x2，则有（ ）| A． | y2＜0＜y1 | B． | y1＜y2＜0 | C． | y1＜0＜y2 | D． | y2＜y1＜0 |
分析 先根据反比例函数y=$\frac{k}{x}$中k＞0可判断出此函数图象在第一、三象限，再根据x1＜0＜x2，可判断出A、B两点所在的象限，根据各象限内点的坐标特点即可判断出y1与y2的大小关系．
解答 解：∵反比例函数y=$\frac{k}{x}$中k＞0，
∴此函数图象在第一、三象限，
∵x1＜0＜x2，
∴A（x1，y1）在第三象限，点B（x2，y2）在第一象限，
∴y1＜0＜y2，
故选C．
点评 本题考查的是反比例函数图象上点的坐标特征及各象限内点的坐标特点，先根据k＞0判断出该函数图象所在象限是解答此题的关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
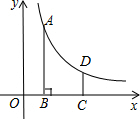如图，在平面直角坐标系中，反比例函数y=$\frac{k}{x}$（x＞0）的图象上有一点A（m，4），过点A作AB⊥x轴于点B，将点B向右平移2个单位长度得到点C，过点C作y轴的平行线交反比例函数的图象于点D，CD=$\frac{4}{3}$
如图，直线y=-$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$交于A、B两点，且点A的坐标为（-6，m），则双曲线y=$\frac{k}{x}$的解析式为y=-$\frac{12}{x}$．
18．同时抛掷三枚质地均匀的硬币，至少有两枚硬币正面向上的概率是（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
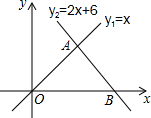如图，直线l1：y1=x和直线l2：y2=-2x+6相交于点A，直线l2与x轴交于点B，动点P沿路线O→A→B运动．