题目内容
12. 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.解:过点E作EF∥AB,
∴∠1=∠B=26°两直线平行,内错角相等
∵AB∥CD(已知),EF∥AB(所作),
∴EF∥CD.(如果两条直线都与第三条直线平行,那么这两条直线也平行 )
∴∠2=∠D=39°(两直线平行,内错角相等)
∴∠BED=∠1+∠2=65°.
分析 作EF∥AB,由于AB∥CD,则可判断AB∥EF∥CD,根据平行线的性质得∠1=∠B=26°,∠2=∠D=39°,于是得到∠BED的度数.
解答 解:过点E作EF∥AB,
∴∠1=∠B=26° (两直线平行,内错角相等)
∵AB∥CD(已知),EF∥AB(所作),
∴EF∥CD.( 如果两条直线都与第三条直线平行,那么这两条直线也平行)
∴∠2=∠D=39°(两直线平行,内错角相等)
∴∠BED=∠1+∠2=65°.
故答案为两直线平行,内错角相等; 如果两条直线都与第三条直线平行,那么这两条直线也平行;两直线平行,内错角相等
点评 本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
3.如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )
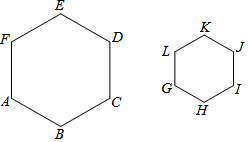

| A. | ∠B=2∠K | |
| B. | 六边形ABCDEF的周长=六边形GHIJKL的周长 | |
| C. | BC=2HI | |
| D. | S六边形ABCDEF=2S六边形GHIJKL |
20. 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.化简$\sqrt{27}+\sqrt{48}$的结果是( )
| A. | $\sqrt{75}$ | B. | $5\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $7\sqrt{3}$ |
 如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.
如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数. 已知:a∥b,∠3=137°,则∠1=137°,∠2=43°.
已知:a∥b,∠3=137°,则∠1=137°,∠2=43°.