题目内容
1.探究:已知m=2$\sqrt{2}$+3,n=2$\sqrt{2}$-3.则(1)m+n=4$\sqrt{2}$;
(2)mn=-1;
(3)m2+n2=34;
(4)m2-n2=24$\sqrt{2}$;
(5)m2-2mn+n2=36.
分析 (1)将m、n的值代入后合并可得;
(2)将m、n的值代入后利用平方差公式计算可得;
(3)将m+n、mn的值代入m2+n2=(m+n)2-2mn计算可得;
(4)将m、n的值代入m2-n2=(m+n)(m-n)计算可得;
(5)将m、n的值代入m2-2mn+n2=(m-n)2计算可得.
解答 解:当m=2$\sqrt{2}$+3,n=2$\sqrt{2}$-3时,
(1)m+n=2$\sqrt{2}$+3+2$\sqrt{2}$-3=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$;
(2)mn=(2$\sqrt{2}$+3)(2$\sqrt{2}$-3)=8-9=-1,
故答案为:-1;
(3)∵m+n=4$\sqrt{2}$,mn=-1,
∴m2+n2=(m+n)2-2mn=(4$\sqrt{2}$)2+2=34,
故答案为:34;
(4)m2-n2=(m+n)(m-n)=(2$\sqrt{2}$+3+2$\sqrt{2}$-3)(2$\sqrt{2}$+3-2$\sqrt{2}$+3)
=4$\sqrt{2}$×6
=24$\sqrt{2}$,
故答案为:24$\sqrt{2}$;
(5)m2-2mn+n2=(m-n)2
=(2$\sqrt{2}$+3-2$\sqrt{2}$+3)2
=36,
故答案为:36.
点评 本题主要考查整式的变形和二次根式的运算,熟练掌握完全平方公式和平方差公式对整式变形及二次根式的性质是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
11. (1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(2)若木棒AB=2米,木棒AB始终保持与地面CD平行,且木棒AB到底面的距离也为1米,类.比(1)的探究方法,填写如表:
(3)平行于地面的线段长度一定,其上方的光源到该线段的距离一定,则当线段逐渐远离地面时,该线段在地面上的影长逐渐变大(填“变大”或“变小”).
 (1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;(2)若木棒AB=2米,木棒AB始终保持与地面CD平行,且木棒AB到底面的距离也为1米,类.比(1)的探究方法,填写如表:
| 光源P到木棒AB的距离 | 木棒AB在地面的影长 |
| 1米 | 4 |
| 2米 | 3 |
| 3米 | $\frac{8}{3}$ |
| …. | |
| 结论:平行于地面的线段长度一定,到地面的距离一定,则其上方的光源逐渐远离线段时,该线段在地面上的影长逐渐变小(填“变大”或“变小”). | |
9.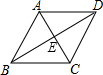 如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
 如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )| A. | ∠ABD=∠ADB | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.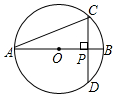 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,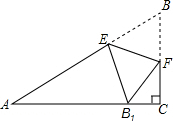 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形. 已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)
已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)