题目内容
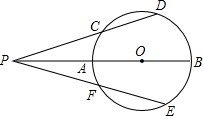 如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.
如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.(1)当P在⊙O外时,求证:CD=EF,PC=PF;
(2)当P在⊙O内时,其它条件不变,画出图形,(1)中结论是否成立?若成立请证明,若不成立说明理由.
考点:垂径定理,角平分线的性质
专题:证明题
分析:(1)证明:作OM⊥CD于M,ON⊥EF于N,连结OD、OE,如图,根据垂径定理得CM=DM,FN=EN,根据角平分线定理由∠DPB=∠EPB得到OM=ON,再证明Rt△ODM≌△OEN得到DM=NE,则Cd=EF,然后证明Rt△OPM≌△OPN得到PM=PN,则PM-CM=PN-FN,则PC=PF;
(2)先画出几何图形,与(1)证明的方法一样,可得到CD=EF,PC=PF.
(2)先画出几何图形,与(1)证明的方法一样,可得到CD=EF,PC=PF.
解答:(1)证明:作OM⊥CD于M,ON⊥EF于N,连结OD、OE,如图,则CM=DM,FN=EN,

∵∠DPB=∠EPB,
∴OM=ON,
在Rt△ODM和△OEN中
,
∴Rt△ODM≌△OEN,
∴DM=NE,
∴CD=EF,
在Rt△OPM和△OPN中,
,
∴Rt△OPM≌△OPN,
∴PM=PN,
∴PM-CM=PN-FN,
即PC=PF;
(2)解:(1)中结论成立.理由如下:
作OM⊥CD于M,ON⊥EF于N,连结OD、OE,如图

∵∠DPB=∠EPB,
∴OM=ON,
在Rt△ODM和△OEN中
,
∴Rt△ODM≌△OEN,
∴DM=NE,
∴CD=EF,
在Rt△OPM和△OPN中,
,
∴Rt△OPM≌△OPN,
∴PM=PN,
∴CM-PM=FN-PN,
即PC=PF.

∵∠DPB=∠EPB,
∴OM=ON,
在Rt△ODM和△OEN中
|
∴Rt△ODM≌△OEN,
∴DM=NE,
∴CD=EF,
在Rt△OPM和△OPN中,
|
∴Rt△OPM≌△OPN,
∴PM=PN,
∴PM-CM=PN-FN,
即PC=PF;
(2)解:(1)中结论成立.理由如下:
作OM⊥CD于M,ON⊥EF于N,连结OD、OE,如图

∵∠DPB=∠EPB,
∴OM=ON,
在Rt△ODM和△OEN中
|
∴Rt△ODM≌△OEN,
∴DM=NE,
∴CD=EF,
在Rt△OPM和△OPN中,
|
∴Rt△OPM≌△OPN,
∴PM=PN,
∴CM-PM=FN-PN,
即PC=PF.
点评:本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了角平分线定理.

练习册系列答案
相关题目
 如图,判断两个三角形是否相似,并求出x和y.
如图,判断两个三角形是否相似,并求出x和y.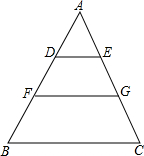 如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC.
如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC. 如图,已知:在△ABC中,D、E是BC上的两点,且AD=BD,AE=CE,∠ADE=82°,∠AED=48°,则∠BAC=
如图,已知:在△ABC中,D、E是BC上的两点,且AD=BD,AE=CE,∠ADE=82°,∠AED=48°,则∠BAC= 如图钢架中,已知∠A=a,焊上等长的钢条BC,CD,DE,EF…来加固钢架,若AB=BC,且这样的钢条最多能焊接5根,那么a的范围是
如图钢架中,已知∠A=a,焊上等长的钢条BC,CD,DE,EF…来加固钢架,若AB=BC,且这样的钢条最多能焊接5根,那么a的范围是