题目内容
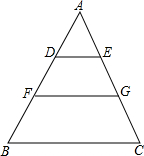 如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC.
如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC.考点:梯形中位线定理,三角形中位线定理
专题:证明题
分析:连接DF与EG的中点M、N,根据三角形的中位线定理,可得出MN=
BC,根据梯形的中位线定理可得出MN=
(DE+FG),从而证得结论;
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:取AB,AC的中点M,N,连接MN,
解:取AB,AC的中点M,N,连接MN,
∴MN=
BC,
∵AD=BF,
∴MN是梯形的中位线,
∴MN=
(DE+FG),
∴DE+FG=BC.
 解:取AB,AC的中点M,N,连接MN,
解:取AB,AC的中点M,N,连接MN,∴MN=
| 1 |
| 2 |
∵AD=BF,
∴MN是梯形的中位线,
∴MN=
| 1 |
| 2 |
∴DE+FG=BC.
点评:本题考查了三角形的中位线定理和梯形的中位线定理,熟练掌握和运用定理是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如下图,D是△ABC的边BC的中点,且
如下图,D是△ABC的边BC的中点,且| AE |
| BE |
| 1 |
| 3 |
| AF |
| FC |
A、
| ||
B、
| ||
C、
| ||
D、
|
点A为数轴上表示-2的动点,当点A沿数轴移动3个单位长到B时,点B所表示的实数是( )
| A、1 | B、-5 |
| C、1或-5 | D、不同于以上答案 |
 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°. 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,现有以下结论:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,现有以下结论: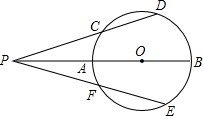 如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.
如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.