题目内容
 如图,判断两个三角形是否相似,并求出x和y.
如图,判断两个三角形是否相似,并求出x和y.考点:相似三角形的判定
专题:
分析:设AE和BD交于点O,可知OD:OB=OE:OA,且∠AOB=∠EOD,所以△AOB∽△EOD,再利用相似三角形的性质可求得x和y的值.
解答: 解:设AE和BD交于点O,如图,
解:设AE和BD交于点O,如图,
则有
=
=
,
=
=
,
∴
=
,且∠AOB=∠EOD,
∴△AOB∽△EOD,
∴
=
,即
=
,
解得x=
,
且∠ABO=∠EDO,
∴y=98.
 解:设AE和BD交于点O,如图,
解:设AE和BD交于点O,如图,则有
| OD |
| OB |
| 26 |
| 39 |
| 2 |
| 3 |
| OE |
| OA |
| 40 |
| 60 |
| 2 |
| 3 |
∴
| OD |
| OB |
| OE |
| OA |
∴△AOB∽△EOD,
∴
| DE |
| AB |
| 2 |
| 3 |
| 27 |
| x |
| 2 |
| 3 |
解得x=
| 81 |
| 2 |
且∠ABO=∠EDO,
∴y=98.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法,及相似三角形的对应边的比等于相似比、对应角相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 作图题:已知平面上四个点A,B,C,D,如图:
作图题:已知平面上四个点A,B,C,D,如图: 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°. 如图,∠A=90°,AB=AC,BC=30cm,则△ABC的面积为
如图,∠A=90°,AB=AC,BC=30cm,则△ABC的面积为 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,现有以下结论:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,现有以下结论: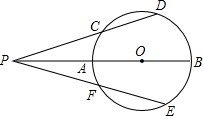 如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.
如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB. 如图,在△ABC中,AD、BE分别为∠BAC、∠ABC的平分线,且交于点F,若点F到AB的距离为3,求点F到△ABC三边的距离的和.
如图,在△ABC中,AD、BE分别为∠BAC、∠ABC的平分线,且交于点F,若点F到AB的距离为3,求点F到△ABC三边的距离的和.