题目内容
已知△ABC中,CD⊥AB于D,∠ACD=15°,CD=
AB,试判断△ABC的形状并说明理由.
| 1 |
| 2 |
考点:含30度角的直角三角形
专题:
分析:首先画出图形,根据三角形内角和定理求出∠A=75°.设CD=a,AD=b,则AB=2CD=2a.在△ACD中,根据正切函数的定义得出tan75°=
=
=2+
,则a=(2+
)b,再由勾股定理求出AC2=AD2+CD2=b2+a2=(8+4
)b2,BC2=BD2+CD2=(2a-b)2+a2=(28+16
)b2,得到AB=BC,从而判定△ABC是等腰三角形.
| CD |
| AD |
| a |
| b |
| 3 |
| 3 |
| 3 |
| 3 |
解答: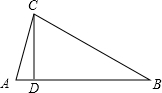 解:△ABC是等腰三角形,理由是:
解:△ABC是等腰三角形,理由是:
如图,∵CD⊥AB于D,∠ACD=15°,
∴∠CDA=∠CDB=90°,∠A=75°.
∵设CD=a,AD=b,则AB=2CD=2a.
在△ACD中,∵tan75°=
=
=2+
,
∴a=(2+
)b,
由勾股定理得,AC2=AD2+CD2=b2+a2=b2+[(2+
)b]2=(8+4
)b2,
在△BCD中,由勾股定理得,BC2=BD2+CD2=(2a-b)2+a2=5a2-4ab+b2=5×[(2+
)b]2-4×(2+
)b•b+b2=(28+16
)b2,
又∵AB2=4a2=4×(2+
)b]2=(28+16
)b2,
∴AB2=BC2,AB=BC,
∴△ABC是等腰三角形.
 解:△ABC是等腰三角形,理由是:
解:△ABC是等腰三角形,理由是:如图,∵CD⊥AB于D,∠ACD=15°,
∴∠CDA=∠CDB=90°,∠A=75°.
∵设CD=a,AD=b,则AB=2CD=2a.
在△ACD中,∵tan75°=
| CD |
| AD |
| a |
| b |
| 3 |
∴a=(2+
| 3 |
由勾股定理得,AC2=AD2+CD2=b2+a2=b2+[(2+
| 3 |
| 3 |
在△BCD中,由勾股定理得,BC2=BD2+CD2=(2a-b)2+a2=5a2-4ab+b2=5×[(2+
| 3 |
| 3 |
| 3 |
又∵AB2=4a2=4×(2+
| 3 |
| 3 |
∴AB2=BC2,AB=BC,
∴△ABC是等腰三角形.
点评:本题考查了勾股定理,正切函数的定义,三角形内角和定理,难度适中.本题利用了tan75°=2+
.
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图是由大小一样的小正方块摆成的立体图形的三视图,它共用( )个小正方块摆成.


| A、5 | B、8 | C、7 | D、6 |
数轴上表示整数的点称为整点.某数轴上的单位长度是1cm,若在这个数轴上随意画出一条长2014cm的线段AB,则线段AB盖住的整点个数是( )
| A、2015个或2016个 |
| B、2014个或2015个 |
| C、2013个或2014个 |
| D、2012个或2013个 |
 已知,如图,BC是圆O的直径,A是弦BD延长线上一点,AC⊥BC于点C,切线DE交AC于点E.
已知,如图,BC是圆O的直径,A是弦BD延长线上一点,AC⊥BC于点C,切线DE交AC于点E. 如图,∠A=90°,AB=AC,BC=30cm,则△ABC的面积为
如图,∠A=90°,AB=AC,BC=30cm,则△ABC的面积为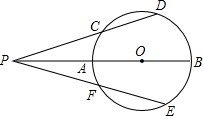 如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.
如图,已知AB直径,P是直线AB上任一点,且∠DPB=∠EPB.