题目内容
11.解方程组(1)$\left\{\begin{array}{l}{2x+y=5}\\{x-2y=0}\end{array}\right.$
(2)$\left\{\begin{array}{l}{4(x-y-1)=3(1-y)-2}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=5①}\\{x-2y=0②}\end{array}\right.$,
由②得:x=2y③,
把③代入①得:4y+y=5,即y=1,
把y=1代入③得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{4x-y=5①}\\{3x+2y=12②}\end{array}\right.$,
①×2+②得:11x=22,即x=2,
把x=2代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1. 如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
 如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )| A. | 70° | B. | 50° | C. | 35° | D. | 25° |
20.下列二次根式中与$\sqrt{3}$是同类二次根式是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{30}$ | C. | $\sqrt{48}$ | D. | $\sqrt{54}$ |
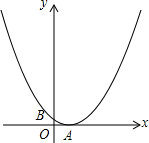 如图,抛物线经过点B(0,1),顶点A在x轴正半轴上,tan∠BAO=$\frac{1}{2}$.
如图,抛物线经过点B(0,1),顶点A在x轴正半轴上,tan∠BAO=$\frac{1}{2}$.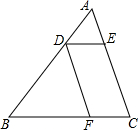 如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.
如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.