题目内容
2.已知x=3+$\sqrt{2}$是一元二次方程2x2-4$\sqrt{2}$x-m=0的一个根,求方程的另一个根及字母m的值.分析 将x=3+$\sqrt{2}$代入到原方程,得出关于m的一元一次方程,解方程即可得出m的值,再根据根与系数的关系得出两根之和,减去已知的方程的根即可得出结论.
解答 解:将x=3+$\sqrt{2}$代入一元二次方程2x2-4$\sqrt{2}$x-m=0中得:
2×$(3+\sqrt{2})^{2}$-4$\sqrt{2}$×(3+$\sqrt{2}$)-m=0,即14-m=0,
解得:m=14.
又∵x1+x2=-$\frac{b}{a}$=2$\sqrt{2}$,且x1=3+$\sqrt{2}$,
∴x2=2$\sqrt{2}$-(3+$\sqrt{2}$)=-3+$\sqrt{2}$.
答:方程的另一个根是-3+$\sqrt{2}$,m的值为14.
点评 本题考查了根与系数的关系以及解一元一次方程,解题的关键是得出关于m的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,由根与系数的关系找出两根之和与两根之积是关键.

练习册系列答案
相关题目
12.计算-(a-b)3(b-a)2的结果为( )
| A. | -(b-a)5 | B. | -(b+a)5 | C. | (a-b)5 | D. | (b-a)5 |
14. 如图,AB∥CD,CB平分∠ABD,若∠C=35°,则∠D的度数为( )
如图,AB∥CD,CB平分∠ABD,若∠C=35°,则∠D的度数为( )
 如图,AB∥CD,CB平分∠ABD,若∠C=35°,则∠D的度数为( )
如图,AB∥CD,CB平分∠ABD,若∠C=35°,则∠D的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
12. 如图所示,该不等式组的解集为( )
如图所示,该不等式组的解集为( )
 如图所示,该不等式组的解集为( )
如图所示,该不等式组的解集为( )| A. | 0<x<1 | B. | x>2 | C. | 1<x<2 | D. | 空集(无解) |
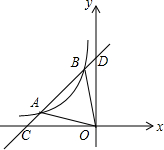 如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$(x<0)的图象交于A(m,n),B(p,q)两点,与两坐标轴交于C,D两点,连接OA,OB.
如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$(x<0)的图象交于A(m,n),B(p,q)两点,与两坐标轴交于C,D两点,连接OA,OB.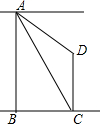 如图,两建筑物AB和CD的水平距离为24米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为16$\sqrt{3}$米.(结果保留根号)
如图,两建筑物AB和CD的水平距离为24米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为16$\sqrt{3}$米.(结果保留根号) 如图,平行四边形ABCD中,AC、BD为对角线且相交于点O,BC=8,BC边上的高为4,求阴影部分的面积.
如图,平行四边形ABCD中,AC、BD为对角线且相交于点O,BC=8,BC边上的高为4,求阴影部分的面积.