题目内容
1.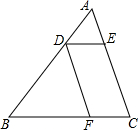 如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.
如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.
分析 根据已知条件得到四边形DECF是平行四边形,根据平行四边形的性质得到DE=CF,根据相似三角形的性质即可得到结论.
解答 解:∵DE∥BC交AC于点E,DF∥AC交BC于点F,
∴四边形DECF是平行四边形,
∴DE=CF,
∵D是AB边的三等分点,
∴$\frac{AD}{AB}=\frac{1}{3}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AD}{AB}$=$\frac{1}{3}$,
∴$\frac{DE}{BF}$=$\frac{1}{2}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
12. 如图所示,该不等式组的解集为( )
如图所示,该不等式组的解集为( )
 如图所示,该不等式组的解集为( )
如图所示,该不等式组的解集为( )| A. | 0<x<1 | B. | x>2 | C. | 1<x<2 | D. | 空集(无解) |
2. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠2与∠4是同旁内角 | B. | ∠1与∠4是内错角 | ||
| C. | ∠3与∠6是同位角 | D. | ∠2与∠5是同位角 |
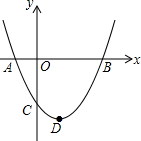 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交点C.在下面五个结论中:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交点C.在下面五个结论中: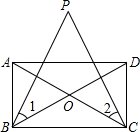 如图,矩形ABCD中,AC与BD相交于O点,∠1=∠2.求证:PB=PC.
如图,矩形ABCD中,AC与BD相交于O点,∠1=∠2.求证:PB=PC.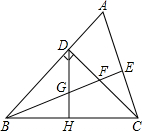 如图,在△ABC中,∠ABC=45°,BE平分∠ABC,且BE⊥AC于点E.
如图,在△ABC中,∠ABC=45°,BE平分∠ABC,且BE⊥AC于点E. 如图,已知Rt△ABC中,∠BAC=90°,∠ACB=30°.
如图,已知Rt△ABC中,∠BAC=90°,∠ACB=30°.