题目内容
8．
如图，已知AD∥BC，∠B=32°，DB平分∠ADE，则∠DEC=（ ）| A． | 64° | B． | 66° | C． | 74° | D． | 86° |
分析 由AD∥BC，∠B=32°，根据平行线的性质，可得∠ADB=32°，又由DB平分∠ADE，可求得∠ADE的度数，继而求得答案．
解答 解：∵AD∥BC，∠B=32°，
∴∠ADB=∠B=32°，
∵DB平分∠ADE，
∴∠ADE=2∠ADB=64°，
∵AD∥BC，
∴∠DEC=∠ADE=64°．
故选：A．
点评 此题考查了平行线的性质以及角平分线的定义，解题时注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
18．
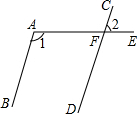如图，AB∥CD，射线AE交CD于点F，若∠1=125°，则∠2的度数是（ ）
如图，AB∥CD，射线AE交CD于点F，若∠1=125°，则∠2的度数是（ ）| A． | 55° | B． | 65° | C． | 75° | D． | 85° |
19．若分式$\frac{x-1}{x+1}$无意义，则x的值是（ ）
| A． | x=1 | B． | x=-1 | C． | x=0 | D． | x≠-1 |
16．当x=3时，分式（$\frac{x^2}{x-1}$-x-1）÷$\frac{x}{{{x^2}-1}}$的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{4}$ |
在正方形网格中，网格线的交点称为格点．如图是3×3的正方形网格，已知A，B是两格点，在网格中找一点C，使得△ABC为等腰直角三角形，则这样的点C有（ ）
20．
某不等式组的解集在数轴上表示如图所示，则这个不等式组可能是（ ）
某不等式组的解集在数轴上表示如图所示，则这个不等式组可能是（ ）| A． | $\left\{\begin{array}{l}x＞4\\ x≤-1\end{array}\right.$ | B． | $\left\{\begin{array}{l}x＜4\\ x≥-1\end{array}\right.$ | C． | $\left\{\begin{array}{l}x＞4\\ x＞-1\end{array}\right.$ | D． | $\left\{\begin{array}{l}x≤4\\ x＞-1\end{array}\right.$ |
17．下列四个几何体中，主视图与俯视图相同的是（ ）
| A． |  | B． |  | C． |  | D． |  |