题目内容
1．若二次根式$\sqrt{3x-2}$有意义，则x的取值范围是（ ）| A． | x≥$\frac{2}{3}$ | B． | x≤$\frac{2}{3}$ | C． | x≥$\frac{3}{2}$ | D． | x≤$\frac{3}{2}$ |
分析 根据二次根式有意义，被开方数大于等于0列式计算即可得解．
解答 解：根据题意得，3x-2≥0，
解得x≥$\frac{2}{3}$．
故选：A．
点评 考查了二次根式的意义和性质．概念：式子$\sqrt{a}$（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．
练习册系列答案
相关题目
如图是甲、乙、丙三人玩跷跷板的示意图（支点在中点处），则甲的体重的取值范围在数轴上表示正确的是（ ）
12．
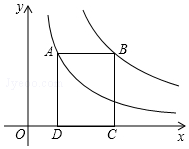如图，点A在双曲线y=$\frac{4}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是9，则k的值为（ ）
如图，点A在双曲线y=$\frac{4}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是9，则k的值为（ ）| A． | 4 | B． | 5 | C． | 9 | D． | 13 |
9．下列计算正确的是（ ）
| A． | a2•a3=a6 | B． | （-2ab）2=4a2b2 | C． | （a2）3=a5 | D． | a6÷a3=a2 |
16．当x=3时，分式（$\frac{x^2}{x-1}$-x-1）÷$\frac{x}{{{x^2}-1}}$的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{4}$ |
10．已知$\frac{x}{y}$=$\frac{3}{4}$，那么下列各式中正确的是（ ）
| A． | $\frac{y}{x+y}$=$\frac{4}{7}$ | B． | $\frac{x}{x-y}$=3 | C． | $\frac{x+2y}{x}$=$\frac{10}{3}$ | D． | $\frac{x-y}{y}$=$\frac{1}{4}$ |
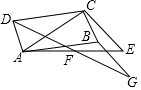如图，已知四边形ABCD为平行四边形，线段CE垂直对角线AC，连接AE，点F为AE中点，连接DF并延长至点G，使FG=DF，连按BG．