题目内容
11.不等式组$\left\{\begin{array}{l}{2x+1≤3}\\{x+3>4}\end{array}\right.$的解集是( )| A. | x>1 | B. | x≤1 | C. | x=1 | D. | 无解 |
分析 先求出不等式的解集,再求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{2x+1≤3①}\\{x+3>4②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x>1,
∴不等式组无解,
故选D.
点评 本题考查了解一元一次不等式组,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如果事件A发生的概率是$\frac{1}{100}$,那么在相同条件下重复试验,下列4种陈述中,不正确的有
①说明做100次这种试验,事件A必发生1次
②说明事件A发生的频率是$\frac{1}{100}$
③说明做100次这种试验中,前99次事件A没发生,后1次事件A才发生
④说明做100次这种试验,事件A可能发生1次( )
①说明做100次这种试验,事件A必发生1次
②说明事件A发生的频率是$\frac{1}{100}$
③说明做100次这种试验中,前99次事件A没发生,后1次事件A才发生
④说明做100次这种试验,事件A可能发生1次( )
| A. | ①、②、③ | B. | ①、②、④ | C. | ②、③、④ | D. | ①、②、③、④ |
19.若分式$\frac{x-1}{x+1}$无意义,则x的值是( )
| A. | x=1 | B. | x=-1 | C. | x=0 | D. | x≠-1 |
16.当x=3时,分式($\frac{x^2}{x-1}$-x-1)÷$\frac{x}{{{x^2}-1}}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
20. 某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )
某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )
 某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )
某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}x>4\\ x≤-1\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<4\\ x≥-1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>4\\ x>-1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x≤4\\ x>-1\end{array}\right.$ |
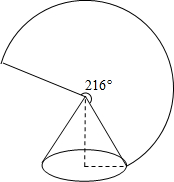 如图,圆锥底面半径为rcm,母线长为5cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
如图,圆锥底面半径为rcm,母线长为5cm,其侧面展开图是圆心角为216°的扇形,则r的值为( ) 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: 在正方形网格中,网格线的交点称为格点.如图是3×3的正方形网格,已知A,B是两格点,在网格中找一点C,使得△ABC为等腰直角三角形,则这样的点C有( )
在正方形网格中,网格线的交点称为格点.如图是3×3的正方形网格,已知A,B是两格点,在网格中找一点C,使得△ABC为等腰直角三角形,则这样的点C有( )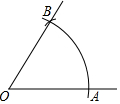 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形.
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形.