题目内容
6.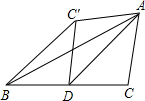 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 6 |
分析 根据折叠前后角相等可知∠CDC′=90°,从而得∠BDC′=90°,在Rt△BDC′中,由勾股定理得BC′=3$\sqrt{2}$.
解答 解:∵把△ADC沿AD对折,点C落在点C′,
∴△ACD≌△AC′D,
∴∠ADC=∠ADC′=45°,DC=DC′,
∴∠CDC′=90°,
∴∠BDC′=90°.
又∵AD为△ABC的中线,BC=6,
∴BD=CD=$\frac{1}{2}$BC=3.
∴BD=DC′=3,即三角形BDC′为等腰直角三角形,
在Rt△BDC′中,由勾股定理得:BC′=$\sqrt{B{D}^{2}+DC{′}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
故选B.
点评 本题考查图形的翻折变换以及勾股定理的运用,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
相关题目
16.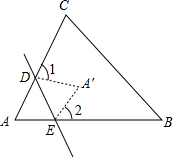 如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
 如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )| A. | α | B. | 2α | C. | 180°-α | D. | 180°-2α |
17.已知x1,x2是方程x2-3x-1=0的两个实数根,那么下列结论正确的是( )
| A. | x1+x2=-1 | B. | x1+x2=-3 | C. | x1+x2=1 | D. | x1+x2=3 |
14.下列四个数中,最小的数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
18.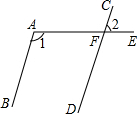 如图,AB∥CD,射线AE交CD于点F,若∠1=125°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=125°,则∠2的度数是( )
 如图,AB∥CD,射线AE交CD于点F,若∠1=125°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=125°,则∠2的度数是( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
15. 如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
16.当x=3时,分式($\frac{x^2}{x-1}$-x-1)÷$\frac{x}{{{x^2}-1}}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
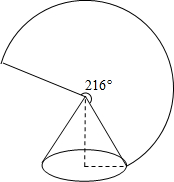 如图,圆锥底面半径为rcm,母线长为5cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
如图,圆锥底面半径为rcm,母线长为5cm,其侧面展开图是圆心角为216°的扇形,则r的值为( ) 如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )


