题目内容
13.若x2+y2+x-y+m=(x+a)2+(y-b)2,则m=$\frac{1}{2}$,ab=$\frac{1}{4}$.分析 由题意可将等式右边分别进行配方,配成右边的形成即可.
解答 解:x2+y2+x-y+m
=(x2+x)+(y2-y)+m
=(x2+x+$\frac{1}{4}$-$\frac{1}{4}$)+(y2-y+$\frac{1}{4}$-$\frac{1}{4}$)+m
=(x+$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2+m-$\frac{1}{2}$
∴(x+$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2+m-$\frac{1}{2}$=(x+a)2+(y-b)2,
∴a=$\frac{1}{2}$,b=$\frac{1}{2}$,m=$\frac{1}{2}$,
∴ab=$\frac{1}{4}$,
故答案为:$\frac{1}{2}$;$\frac{1}{4}$;
点评 本题考查完全平公式,涉及分组分解、代入求值等知识.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
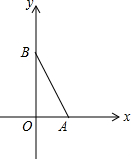 如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.
如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.