题目内容
3.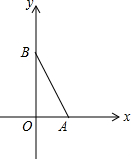 如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.
如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.
分析 (1)先求出A、B两点坐标,利用待定系数法即可解决问题.
(2)如图1中,由题意可知,C(3,1),作CG∥OB交抛物线于G.x=3时,y=2,推出点G坐标(3,2),所以把抛物线向下平移1个单位即可经过点C,由此即可解决问题.
(3)如图2中,设P(m,m2-3m+1),由题意BB1=DD1,△PBB1的面积是△PDD1面积的2倍,可得m=2|$\frac{3}{2}$-m|,解方程即可.
解答 解:(1)∵二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2,
∴B(0,2),A(1,0),
把A(1,0)代入y=x2+mx+2得m=-3,
∴二次函数的解析式为y=x2-3x+2.
(2)如图1中,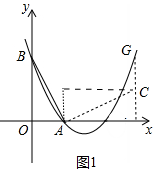
由题意可知,C(3,1),作CG∥OB交抛物线于G.
x=3时,y=2,
∴点G坐标(3,2),
∴把抛物线向下平移1个单位即可经过点C,
∴平移后的抛物线的解析式为y=x2-3x+1.
(3)如图2中,设P(m,m2-3m+1),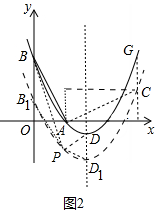
∵BB1=DD1,△PBB1的面积是△PDD1面积的2倍,
∴m=2|$\frac{3}{2}$-m|,
∴m=1或3,
∴点P坐标为(1,-1)或(3,1).
点评 本题考查二次函数综合题、待定系数法、旋转变换.平移变换、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会寻找特殊点解决问题,学会用方程的思想思考问题,所以中考压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为40°.
如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为40°.