题目内容
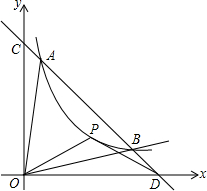
 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
(1)试确定上述反比例函数和一次函数的表达式;
(2)求
| AC |
| BC |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据A的坐标求出m的值,得出反比例函数的解析式,把B的坐标代入求出B的坐标,代入一次函数的解析式求出即可;
(2)根据A、B、C的坐标根据勾股定理求出AC、BC的值,代入求出即可.
(2)根据A、B、C的坐标根据勾股定理求出AC、BC的值,代入求出即可.
解答:解:(1)依题意,m=-2×1=-2,
∴反比例函数为y=-
,
把B(1,n)代入得:n=-
=-2,
∴
,
解得:k=b=-1,
∴一次函数为y=-x-1;
(2)把y=0代入得:0=-x-1,
解得:x=-1,
即C点的坐标为C(-1,0),
∵A(-2,1),B(1,-2),
∴AC=
=
,BC=
=2
∴
=
=
.
∴反比例函数为y=-
| 2 |
| x |
把B(1,n)代入得:n=-
| 2 |
| 1 |
∴
|
解得:k=b=-1,
∴一次函数为y=-x-1;
(2)把y=0代入得:0=-x-1,
解得:x=-1,
即C点的坐标为C(-1,0),
∵A(-2,1),B(1,-2),
∴AC=
| 12+(-1+2)2 |
| 2 |
| 22+(1+1)2 |
| 2 |
∴
| AC |
| BC |
| ||
2
|
| 1 |
| 2 |
点评:本题考查了勾股定理,用待定系数法求反比例函数和一次函数的解析式,一次函数和反比例函数的交点问题的应用,题目是一道比较典型的题目,难度适中.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y= 我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y= 如图,已知∠1=∠2,∠3=∠4,△ABC与△DCB全等吗?为什么?
如图,已知∠1=∠2,∠3=∠4,△ABC与△DCB全等吗?为什么?