题目内容
 我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=| k |
| x+2 |
| k |
| x |
如图,已知反比例函数y=
| 4 |
| x |
(1)写出点B的坐标,并求a的值;
(2)将函数y=
| 4 |
| x |
①求n的值;
②分别写出平移后的两个图象C′和l′对应的函数关系式;
③直接写出不等式
| 4 |
| x-1 |
考点:反比例函数综合题
专题:
分析:1)直接把A点坐标代入y=ax即可求出a的值;利用反比例函数的图象与正比例函数的图象的交点关于原点对称确定B点坐标;
(2)①根据题意得到函数y=
的图象向右平移n(n>0)个单位长度,得到的图象C′的解析式为y=
,然后把M点坐标代入即可得到n的值;
②根据题意易得图象C′的解析式为y=
;图象l′的解析式为y=x-1;
③不等式
≤ax-1可理解为比较y=
和y=x-1的函数值,由于y=
和y=x-1为函数y=
的图象和直线AB同时向右平移1个单位长度,得到的图象;而反比例函数y=
的图象与正比例函数y=ax(a≠0)的图象的交点为A(2,2)和B(-2,-2),所以平移后交点分别为(3,2)和B(-1,-2),则当x<-1或0<x<2时,函数y=
的图象都在y=x-1的函数图象上方.
(2)①根据题意得到函数y=
| 4 |
| x |
| 4 |
| x-n |
②根据题意易得图象C′的解析式为y=
| 4 |
| x-1 |
③不等式
| 4 |
| x-1 |
| 4 |
| x-1 |
| 4 |
| x-1 |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x-1 |
解答:解:(1)把A(2,2)代入y=ax得 2a=2,
解得a=1.
∵反比例函数y=
的图象与正比例函数y=x的图象的交点关于原点对称,
∴B点坐标为(-2,-2);
(2)①函数y=
的图象向右平移n(n>0)个单位长度,得到的图象C′的解析式为y=
,
把M(2,4)代入得4=
,解得n=1;
②图象C′的解析式为y=
;图象l′的解析式为y=x-1;
③不等式
≤ax-1的解集是x≥3或-1≤x<1.
解得a=1.
∵反比例函数y=
| 4 |
| x |
∴B点坐标为(-2,-2);
(2)①函数y=
| 4 |
| x |
| 4 |
| x-n |
把M(2,4)代入得4=
| 4 |
| 2-n |
②图象C′的解析式为y=
| 4 |
| x-1 |
③不等式
| 4 |
| x-1 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、会确定反比例函数与一次函数的交点坐标以及待定系数法确定解析式;会运用图形的平移确定点的坐标和同时提高阅读理解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图:△ABC和△CDE是等边三角形.求证:BE=AD.
如图:△ABC和△CDE是等边三角形.求证:BE=AD.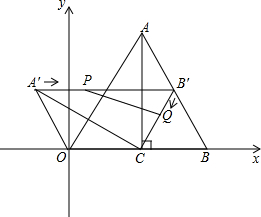 如图,在平面直角坐标系中,Rt△AOC的顶点O在坐标原点,直角顶点C在x轴的正半轴上,顶点A在第一象限.以AC为轴将△AOC翻折得到△ACB,然后将△ACB绕点C逆时针旋转60°,得到△A′CB′.已知OA=4cm,∠OAC=30°.
如图,在平面直角坐标系中,Rt△AOC的顶点O在坐标原点,直角顶点C在x轴的正半轴上,顶点A在第一象限.以AC为轴将△AOC翻折得到△ACB,然后将△ACB绕点C逆时针旋转60°,得到△A′CB′.已知OA=4cm,∠OAC=30°. 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=