题目内容
17．下列计算正确的是（ ）| A． | x4+x4=2x8 | B． | （x2y）3=x6y | C． | -（x2）3=x5 | D． | -x3•（-x）5=x8 |
分析 结合同底数幂的乘法，幂的乘方与积的乘方的概念和运算法则进行求解即可．
解答 解：A、x4+x4=2x4≠2x8，本选项错误；
B、（x2y）3=x6y3≠x6y，本选项错误；
C、-（x2）3=-x6≠x5，本选项错误；
D、-x3•（-x）5=x8，本选项正确．
故选D．
点评 本题考查了幂的乘方与积的乘方，解答本题的关键在于熟练掌握该知识点的概念和运算法则．
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
7．下列各式从左到右的变形中，是因式分解的为（ ）
| A． | x2-1+y2=（x-1）（x+1）+y2 | B． | x（a-b）=ax-bx | ||
| C． | ax+bx+c=x（a+b）+c | D． | x2-1=（x+1）（x-1） |
8．一元二次方程x2=4x的根是（ ）
| A． | x=4 | B． | x=2 | C． | x=0或x=4 | D． | x=±2 |
5．下列选项中，与ab2c3是同类项的是（ ）
| A． | ab2 | B． | -$\frac{a{b}^{2}{c}^{3}}{7}$ | C． | 2abc | D． | -$\frac{a{b}^{2}+{c}^{3}}{2}$ |
12．
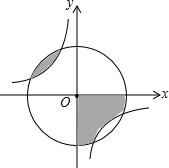如图，反比例函数y=$\frac{k}{x}$（k＜0）的图象与⊙O相交，某同学在⊙O内做随机扎针实验，针头落在阴影区域的概率是（ ）
如图，反比例函数y=$\frac{k}{x}$（k＜0）的图象与⊙O相交，某同学在⊙O内做随机扎针实验，针头落在阴影区域的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | -$\frac{1}{k}$ | D． | $\frac{1}{π}$ |
2．
如图是正方体的一个平面展开图，如果原正方体上前面的字为“友”，则后面的字为（ ）
如图是正方体的一个平面展开图，如果原正方体上前面的字为“友”，则后面的字为（ ）| A． | 善 | B． | 国 | C． | 诚 | D． | 爱 |
9．已知Rt△ABC中，∠C=90°，AC=3，BC=4，若以2为半径作⊙C，则斜边AB与⊙C的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 无法确定 |
6．
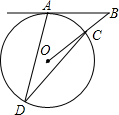如图，在⊙O中，AD，CD是弦，连接OC并延长，交过点A的切线于点B，若∠ADC=30°，则∠ABO的度数为（ ）
如图，在⊙O中，AD，CD是弦，连接OC并延长，交过点A的切线于点B，若∠ADC=30°，则∠ABO的度数为（ ）| A． | 50° | B． | 40° | C． | 30° | D． | 20° |
7．在一个口袋中装有4个完全相同的小球，它们的标号分别为1、2、3、4，从中随机摸出一个小球记下标号放回，再从中随机摸出一个小球，则两次摸出的小球的标号之和大于4的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{8}$ | C． | $\frac{3}{4}$ | D． | $\frac{5}{8}$ |