题目内容
16．如图，先将一张长方形的纸沿虚线对折，再对折，然后按图中虚线剪下，将剪下的纸展开，一定可以得到一个（ ）
| A． | 菱形 | B． | 矩形 | C． | 正方形 | D． | 梯形 |
分析 根据题意知，对折实际上就是对称，对折两次的话，剪下应有4条边，并且这4条边还相等，从而可以进行从题后的答案中选择．
解答 解：由题意知，对折实际上就是对称，对折2次的话，剪下应有4条边，并且这4条边还相等，只有菱形满足这一条件．
故选：A．
点评 此题考查了利用对称设计图案以及菱形的判定，关键是根据对折实际上就是轴对称性质的运用进行解答．
练习册系列答案
相关题目
7．下列各式从左到右的变形中，是因式分解的为（ ）
| A． | x2-1+y2=（x-1）（x+1）+y2 | B． | x（a-b）=ax-bx | ||
| C． | ax+bx+c=x（a+b）+c | D． | x2-1=（x+1）（x-1） |
如图，将一副三角尺的直角顶点叠放在点C处，∠D=30°，∠B=45°，求：
1．
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）| A． | $\frac{AB}{BP}$=$\frac{AC}{CB}$ | B． | ∠APB=∠ABC | C． | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D． | ∠ABP=∠C |
8．一元二次方程x2=4x的根是（ ）
| A． | x=4 | B． | x=2 | C． | x=0或x=4 | D． | x=±2 |
5．下列选项中，与ab2c3是同类项的是（ ）
| A． | ab2 | B． | -$\frac{a{b}^{2}{c}^{3}}{7}$ | C． | 2abc | D． | -$\frac{a{b}^{2}+{c}^{3}}{2}$ |
6．
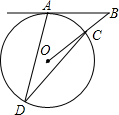如图，在⊙O中，AD，CD是弦，连接OC并延长，交过点A的切线于点B，若∠ADC=30°，则∠ABO的度数为（ ）
如图，在⊙O中，AD，CD是弦，连接OC并延长，交过点A的切线于点B，若∠ADC=30°，则∠ABO的度数为（ ）| A． | 50° | B． | 40° | C． | 30° | D． | 20° |