题目内容
17.关于x的方程$\frac{a}{x-3}$=2的解是正数,则a的取值范围是a>-6且a≠0.分析 分式方程去分母转化为整式方程,求出整式方程的解表示出x,即可确定出a的范围.
解答 解:去分母得:a=2x-6,即x=$\frac{a+6}{2}$,
由分式方程的解为正数,得到$\frac{a+6}{2}$>0,且$\frac{a+6}{2}$≠3,
解得:a>-6且a≠0,
故答案为:a>-6且a≠0
点评 此题考查了分式方程的解,需注意在任何时候都要考虑分母不为0.

练习册系列答案
相关题目
20.某水果店计划购进甲、乙两种新出产的水果共140千克,这两种水果的进价,售价如表所示,该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,当购进甲种水果35千克时利润最大.
| 进价(元/千克) | 售价(元/千克) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
2.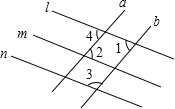 如图,下面说法正确的是( )
如图,下面说法正确的是( )
 如图,下面说法正确的是( )
如图,下面说法正确的是( )| A. | 如果∠1+∠3=180°,则l∥n | B. | 如果∠2=∠4,则a∥b | ||
| C. | 如果∠1=∠4,则l∥m | D. | 如果∠2=∠3,则m∥n |
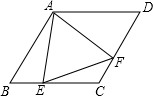 如图所示,在菱形ABCD中,E,F分别是BC,CD上的点,且∠B=∠EAF=60°.求证:AE=AF.
如图所示,在菱形ABCD中,E,F分别是BC,CD上的点,且∠B=∠EAF=60°.求证:AE=AF.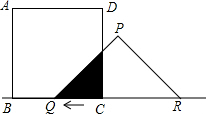 如图,有一边长为5的正方形ABCD和一等腰△PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重叠部分的面积为S.
如图,有一边长为5的正方形ABCD和一等腰△PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重叠部分的面积为S.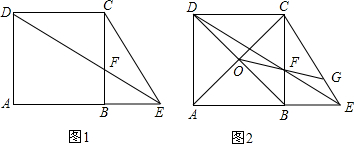
 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.