题目内容
20.某水果店计划购进甲、乙两种新出产的水果共140千克,这两种水果的进价,售价如表所示,该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,当购进甲种水果35千克时利润最大.| 进价(元/千克) | 售价(元/千克) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
分析 利用两种水果每千克的利润表示出总利润,再利用一次函数增减性得出最大值即可.
解答 解:由图表可得:甲种水果每千克利润为:3元,乙种水果每千克利润为:4元,
设总利润为W,由题意可得出:W=3x+4(140-x)=-x+560,
故W随x的增大而减小,则x越小W越大,
因为该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,
∴140-x≤3x,
解得:x≥35,
∴当x=35时,W最大=-35+560=525(元),
故140-35=105(kg).
答:当甲购进35千克,乙种水果105千克时,此时利润最大为525元.
故答案为:35.
点评 主要考查了一次函数的应用,利用一次函数增减性得出函数最值是解题关键.

练习册系列答案
相关题目
12. 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )| A. | 作中线AD,再取AD的中点O | |
| B. | 分别作AB、BC的高线,再取此两高线的交点O | |
| C. | 分别作中线AD、BE,再取此两中线的交点O | |
| D. | 分别作∠A、∠B的角平分线,再取此两角平分线的交点O |
9.一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
 小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是58度.
小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是58度.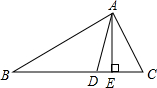 如图,在△ABC中,已知∠C=60°,∠B=40°,AD是△ABC的角平分线,AE是△ABC的高线,则∠DAE的度数为10°.
如图,在△ABC中,已知∠C=60°,∠B=40°,AD是△ABC的角平分线,AE是△ABC的高线,则∠DAE的度数为10°.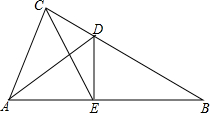 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.