题目内容
1.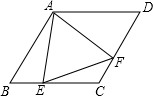 如图所示,在菱形ABCD中,E,F分别是BC,CD上的点,且∠B=∠EAF=60°.求证:AE=AF.
如图所示,在菱形ABCD中,E,F分别是BC,CD上的点,且∠B=∠EAF=60°.求证:AE=AF.
分析 连结AC,如图,根据菱形的性质得AB=BC,而∠B=60°,则可判定△ABC为等边三角形,得到∠2=60°,∠1+∠4=60°,AC=AB,易得∠ACF=60°,∠1=∠3,然后利用“ASA”可证明△AEB≌△AFC,于是得到AE=AF.
解答 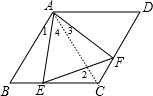 证明:连结AC,如图,
证明:连结AC,如图,
∵四边形ABCD为菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠2=60°,∠1+∠4=60°,AC=AB,
∴∠ACF=60°,
∵∠EAF=60°,即∠3+∠4=60°,
∴∠1=∠3,
在△AEB和△AFC中,
$\left\{\begin{array}{l}{∠1=∠3}\\{AB=AC}\\{∠B=∠ACD}\end{array}\right.$,
∴△AEB≌△AFC,
∴AE=AF.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
12.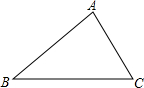 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )| A. | 作中线AD,再取AD的中点O | |
| B. | 分别作AB、BC的高线,再取此两高线的交点O | |
| C. | 分别作中线AD、BE,再取此两中线的交点O | |
| D. | 分别作∠A、∠B的角平分线,再取此两角平分线的交点O |
9.一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
16.某人上山后,立即下山,已知下山的速度是上山速度的3倍,则此人上下山的平均速度是上山速度的( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
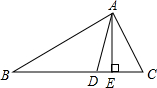 如图,在△ABC中,已知∠C=60°,∠B=40°,AD是△ABC的角平分线,AE是△ABC的高线,则∠DAE的度数为10°.
如图,在△ABC中,已知∠C=60°,∠B=40°,AD是△ABC的角平分线,AE是△ABC的高线,则∠DAE的度数为10°.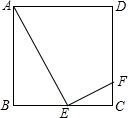 如图,正方形ABCD的边长为1,动点E在BC上,∠AEF=90°,EF交DC于F,当线段FC最长时,BE的长为$\frac{1}{2}$.
如图,正方形ABCD的边长为1,动点E在BC上,∠AEF=90°,EF交DC于F,当线段FC最长时,BE的长为$\frac{1}{2}$.