题目内容
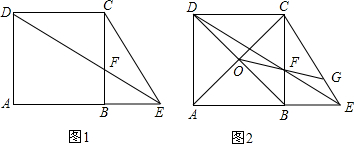
12.如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE=x,CF=y.(1)求y关于x的函数解析式,并写出x的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证:∠CEB=∠COG;
(3)在(2)的条件下,当OG=$\frac{2\sqrt{5}}{5}$时,求x的值.
分析 (1)根据正方形的性质证明△DCF∽△EBF,得到成比例线段,代入x、y可以得到y关于x的函数解析式;
(2)由(1)的结论求出CF•AE的值,根据正方形的性质求出AC•CO的值,证明△OCF∽△EAC,得到答案;
(3)根据勾股定理求出CE,证明△OCG∽△ECA,得到比例式求出x的值.
解答 解:(1)∵四边形ABCD是正方形,∴DC∥AB,
∴$\frac{DC}{BE}$=$\frac{CF}{BF}$,即$\frac{1}{x}$=$\frac{y}{1-y}$,
∴y=$\frac{1}{x+1}$,x的取值范围是x>0;
(2)∵CF•AE=$\frac{1}{x+1}$•(x+1)=1,
CA•CO=$\sqrt{2}$•$\frac{\sqrt{2}}{2}$=1,
∴CF•AE=CA•CO,即$\frac{CF}{AC}$=$\frac{CO}{AE}$,
又∠OCF=∠EAC=45°,
∴△OCF∽△EAC,
∴∠CEB=∠COG;
(3)在Rt△CBE中,CE=$\sqrt{1+{x}^{2}}$,∵∠CEB=∠COG,∠ECA=∠ECA,
∴△OCG∽△ECA,
∴$\frac{OG}{AE}$=$\frac{CO}{CE}$,即$\frac{\frac{2\sqrt{5}}{5}}{1+x}$=$\frac{\frac{\sqrt{2}}{2}}{\sqrt{1+{x}^{2}}}$,
解得,x1=$\frac{1}{3}$,x2=3,
经检验,它们都是方程的根,
∴x的值为3或$\frac{1}{3}$.
点评 本题考查的是相似三角形的判定和性质、正方形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
16.某人上山后,立即下山,已知下山的速度是上山速度的3倍,则此人上下山的平均速度是上山速度的( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |