题目内容
12.某服装店5400元购进A,B两种童装,按标价全部售出后的总利润是3000元(利润=售价-进价),这两种服装进价、标价如表所示:| 类型价格 | A型 | B型 |
| 进价(元/件) | 50 | 80 |
| 标价(元/件) | 80 | 120 |
(2)如果A种童装按标价的八折出售,B种童装在标价基础上再降价30元出售.那么这批童装全部售完后,童装店共获得多少利润?
分析 (1)设A型童装购进x件,B型童装购进y件,根据总价=单价×数量结合总利润=单件利润×数量即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据总利润=A型童装单件利润×数量+B型童装单件利润×数量,代入数据即可得出结论.
解答 解:(1)设A型童装购进x件,B型童装购进y件,
根据题意得:$\left\{\begin{array}{l}{50x+80y=5400}\\{(80-50)x+(120-80)y=3000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=60}\\{y=30}\end{array}\right.$.
答:A型童装购进60件,B型童装购进30件.
(2)(80×0.8-50)×60+(120-80-30)×30=14×60+10×30=1140(元).
答:这批童装全部售完后,童装店共获得1140元利润.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)根据数量关系列出关于x、y的二元一次方程组;(2)根据数量关系列式计算.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
4.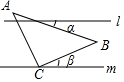 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
2.下列分式中,最简分式是( )
| A. | $\frac{2}{x-2}$ | B. | $\frac{2}{4x}$ | C. | $\frac{y-x}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-4x+4}{x-2}$ |
 如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.
如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.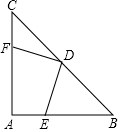 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.