题目内容
2. 在平面直角坐标系xOy中,点A、B、C的坐标分别为(-1,0)、(-2,3)、(-3,1).(1)作出△ABC关于x轴对称的△A1B1C1,直接写出B1、C1两点的坐标:B1(-2,-3) C1(-3,-1).
在平面直角坐标系xOy中,点A、B、C的坐标分别为(-1,0)、(-2,3)、(-3,1).(1)作出△ABC关于x轴对称的△A1B1C1,直接写出B1、C1两点的坐标:B1(-2,-3) C1(-3,-1).(2)写出△ABC的面积,S△ABC=2.5.
(3)在y轴上找一点D,使得BD+DA的值最小,求D点的坐标.
分析 (1)分别作出点B、C关于x的轴的对称点,顺次连接即可得;
(2)割补法求解可得;
(3)作点B关于y轴的对称点B′,连接AB′,交y轴于点D,即可得点D的坐标.
解答 解:(1)如图,△A1B1C1即为所求,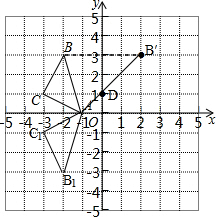
由图可知,B1(-2,-3),C1(-3,1),
故答案为:-2、-3,-3、-1.
(2)S△ABC=2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2=2.5,
故答案为:2.5;
(3)作点B关于y轴的对称点B′,连接AB′,交y轴于点D,可得D(0,1).
点评 本题主要考查轴对称作图及轴对称-最短路线问题,熟练掌握轴对称的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列结论中,不能由a+b=0得到的是( )
| A. | a2=-ab | B. | a=0,b=0 | C. | |a|=|b| | D. | a2=b2 |
14.下列运算中,错误的是( )
| A. | $\sqrt{3+5}$=$\sqrt{3}$+$\sqrt{5}$ | B. | $\sqrt{3×5}$=$\sqrt{3}$×$\sqrt{5}$ | C. | $\frac{\sqrt{24}}{\sqrt{6}}$=$\sqrt{\frac{24}{6}}$ | D. | ($\sqrt{2}$)3=2$\sqrt{2}$ |
11.△ABC中,∠A,∠B均为锐角,且有|tan2B-3|+(2sinA-$\sqrt{3}$)2=0,则△ABC是( )
| A. | 直角(不等腰)三角形 | B. | 等边三角形 | ||
| C. | 等腰(不等边)三角形 | D. | 等腰直角三角形 |
 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.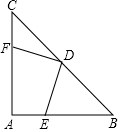 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.