题目内容
对任意实数x,[x]表示不超过x的最大整数,如果[x]=3,[y]=1,[z]=1,那么[x+y-z]的值等于 .
考点:取整计算
专题:计算题
分析:根据[x]=3,[y]=1,[z]=1,可得出x、y、z的范围,然后可得出x+y-z的范围,继而根据取整函数的定义可得出答案.
解答:解:∵[x]=3,[y]=1,[z]=1,
∴3<x<4,1<y<2,1<z<2,
∴2<x+y-z<5,
故可得出[x+y-z]=2,3,4.
故答案为:2或3或4.
∴3<x<4,1<y<2,1<z<2,
∴2<x+y-z<5,
故可得出[x+y-z]=2,3,4.
故答案为:2或3或4.
点评:此题考查了取整函数的知识,解答本题关键是根据取整函数的定义得出x、y、z的范围,及(x+y-z)的范围,难度一般.

练习册系列答案
相关题目
 如图,已知AB=a,BD=b,(a、b为常数),BC=BD,∠ABD:∠BAC:∠ACD:∠CBD=1:2:4:4.
如图,已知AB=a,BD=b,(a、b为常数),BC=BD,∠ABD:∠BAC:∠ACD:∠CBD=1:2:4:4. 某厂承印新课程标准实验教材,新书出厂时,要将打包成长、宽、高分别为x分米、y分米、z分米的长方体包装加上扎带(如图所示双虚线位置).若扎带每个接头处要多余0.5分米,则一个长方体包装上的扎带总长
某厂承印新课程标准实验教材,新书出厂时,要将打包成长、宽、高分别为x分米、y分米、z分米的长方体包装加上扎带(如图所示双虚线位置).若扎带每个接头处要多余0.5分米,则一个长方体包装上的扎带总长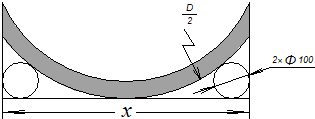 两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.
两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm. 如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为
如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为