题目内容
如图,在平台上用直径为100mm的两根圆钢棒嵌在大型工件的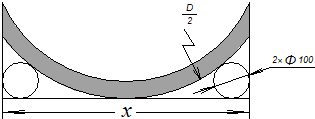 两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.
两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.
(1)求出D(mm)与x(mm)之间的函数关系式;
(2)当图形工件的直径D小于圆钢棒的直径时,上面所求得的D与x的函数关系式还是否仍然适用?请说明理由.
 两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.
两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.(1)求出D(mm)与x(mm)之间的函数关系式;
(2)当图形工件的直径D小于圆钢棒的直径时,上面所求得的D与x的函数关系式还是否仍然适用?请说明理由.
考点:相切两圆的性质,勾股定理,切线的性质
专题:计算题
分析:(1)设三圆的圆心分别为A、B、C,连接AB,则AB过切点E,连接AC,则AC过切点F,连接BC,AN,AN交BC于M,由题意得出AB=AC=50+
,BC=x-(50+50)=x-100,AN=
-50,在△ABM中根据勾股定理得出D和x的方程,求出即可;
(2)根据(1)结合图形仍能得出函数解析式,即可得出答案.
| D |
| 2 |
| D |
| 2 |
(2)根据(1)结合图形仍能得出函数解析式,即可得出答案.
解答:(1)解: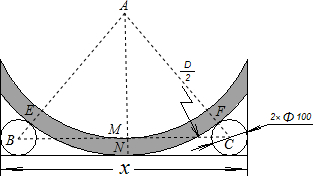
如图设三圆的圆心分别为A、B、C,连接AB,则AB过切点E,连接AC,则AC过切点F,连接BC,AN,AN交BC于M,
由题意得:AB=AC=50+
,BC=x-(50+50)=x-100,AN=
-50,
∵AC=AB,AM⊥BC,
∴BM=CM=
(x-100)=
x-50,
在Rt△ABM中,由勾股定理得:AB2=AM2+BM2,
∴(50+
)2=(
-50)2+(
x-50)2,
即D=
x2-
x+25.
(2)解:当图形工件的直径D小于圆钢棒的直径时,上面所求得的D与x的函数关系式能仍然适用,
因为那样时,三圆同时与平台相切,有两大圆都与小圆相切时,得出的方程与(1)中的方程相同,
所有上面所求得的D与x的函数关系式能仍然适用.

如图设三圆的圆心分别为A、B、C,连接AB,则AB过切点E,连接AC,则AC过切点F,连接BC,AN,AN交BC于M,
由题意得:AB=AC=50+
| D |
| 2 |
| D |
| 2 |
∵AC=AB,AM⊥BC,
∴BM=CM=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABM中,由勾股定理得:AB2=AM2+BM2,
∴(50+
| D |
| 2 |
| D |
| 2 |
| 1 |
| 2 |
即D=
| 1 |
| 400 |
| 1 |
| 2 |
(2)解:当图形工件的直径D小于圆钢棒的直径时,上面所求得的D与x的函数关系式能仍然适用,
因为那样时,三圆同时与平台相切,有两大圆都与小圆相切时,得出的方程与(1)中的方程相同,
所有上面所求得的D与x的函数关系式能仍然适用.
点评:本题考查了相切两圆的性质,切线的性质,勾股定理等知识点的应用,能根据题意得出方程是解此题的关键,主要考查学生的观察能力和构造直角三角形的能力,题目比较典型,有一定的难度.

练习册系列答案
相关题目
有一旅客携带了30kg行李从南京国际机场乘飞机去天津,按民航规定,旅客最多可免费携带20kg行李,超过部分每公斤按飞机票价的1.5%购买行李票,现该旅客购买了120元的行李票,则他的飞机票价格应是( )元.
| A、800 | B、1000 |
| C、1600 | D、2400 |
由四名同学每人书写一个不同的实系数一元二次方程,他们所提供的四个方程中恰好有两个方程没有实数根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
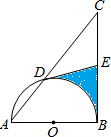 如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-6x+8=0的两个根,则图中阴影部分的面积为
如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-6x+8=0的两个根,则图中阴影部分的面积为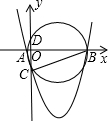 如图,已知二次函数y=(x+m)2+k-m2的图象与x轴交于两不同点A(x1,0)、B(x2,0),与y轴的交点为C.则△ABC的外接圆与y轴的另一个交点D的坐标是
如图,已知二次函数y=(x+m)2+k-m2的图象与x轴交于两不同点A(x1,0)、B(x2,0),与y轴的交点为C.则△ABC的外接圆与y轴的另一个交点D的坐标是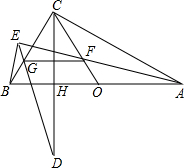 如图,O是Rt△ABC斜边AB的中点,CH⊥AB于H,延长CH至D,使得CH=DH,F为CO上任意一点,过B作BE⊥AF于E,连接DE交BC于G.
如图,O是Rt△ABC斜边AB的中点,CH⊥AB于H,延长CH至D,使得CH=DH,F为CO上任意一点,过B作BE⊥AF于E,连接DE交BC于G.