题目内容
已知实数a、b满足条件：a2-7a+2=0，b2-7b+2=0，那么代数式a2+b2-7(a+b)+
+
的值为 ．
| b |
| a |
| a |
| b |
考点：根与系数的关系
专题：
分析：由实数a，b满足条件a2-7a+2=0，b2-7b+2=0，可把a，b看成是方程x2-7x+2=0的两个根，再利用根与系数的关系即可求解．
解答：解：由实数a，b满足条件a2-7a+2=0，b2-7b+2=0，
∴可把a，b看成是方程x2-7x+2=0的两个根，
∴a+b=7，ab=2，
∴a2+b2-7(a+b)+
+
=（a+b）2-2ab-7（a+b）+
=49-4-49+
=
．
故答案为：
．
∴可把a，b看成是方程x2-7x+2=0的两个根，
∴a+b=7，ab=2，
∴a2+b2-7(a+b)+
| b |
| a |
| a |
| b |
=（a+b）2-2ab-7（a+b）+
| (a+b)2-2ab |
| ab |
=49-4-49+
| 45 |
| 2 |
=
| 37 |
| 2 |
故答案为：
| 37 |
| 2 |
点评：本题考查了根与系数的关系，属于基础题，关键是把a，b看成方程的两个根后再根据根与系数的关系解题．
练习册系列答案
相关题目
有一旅客携带了30kg行李从南京国际机场乘飞机去天津，按民航规定，旅客最多可免费携带20kg行李，超过部分每公斤按飞机票价的1.5%购买行李票，现该旅客购买了120元的行李票，则他的飞机票价格应是（ ）元．
| A、800 | B、1000 |
| C、1600 | D、2400 |
由四名同学每人书写一个不同的实系数一元二次方程，他们所提供的四个方程中恰好有两个方程没有实数根的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
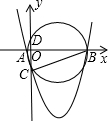如图，已知二次函数y=（x+m）2+k-m2的图象与x轴交于两不同点A（x1，0）、B（x2，0），与y轴的交点为C．则△ABC的外接圆与y轴的另一个交点D的坐标是