题目内容
6.己知四边形ABCD是平行四边形,E是AD上一点且CE平分∠BCD,BE⊥CE.求证:BC=2CD.分析 延长CE交BA的延长线于F,先证明CD=ED,BF=BC,再证明CE=EF,由AF∥CD,得出AE=ED,即可得出结论.
解答 证明:延长CE交BA的延长线于F;如图所示: ∵CE平分∠BCD,
∵CE平分∠BCD,
∴∠1=∠2,
∵四边形ABCD是平行四边形,
∴BC=AD,AD∥BC,BF∥CD,
∴∠1=∠3,∠2=∠4,
∴∠2=∠3,∠1=∠4,
∴CD=ED,BF=BC,
∵BE⊥CE,
∴CE=EF,
∵AF∥CD,
∴AE=ED,
∴BC=AD=2ED=2CD.
点评 本题考查了平行四边形的性质、等腰三角形的判定与性质;证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
相关题目
 矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.
矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.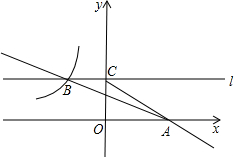 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{3}$+b与x轴交于点A,与双曲线y=-$\frac{6}{x}$在第二象限内交于点B(-3,a).
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{3}$+b与x轴交于点A,与双曲线y=-$\frac{6}{x}$在第二象限内交于点B(-3,a).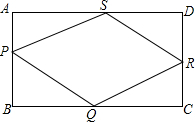 已知,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点在矩形边上.
已知,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点在矩形边上.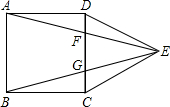 如图,在正方形ABCD外侧,以CD为一边作等边三角形CDE,连接AE,BE
如图,在正方形ABCD外侧,以CD为一边作等边三角形CDE,连接AE,BE