题目内容
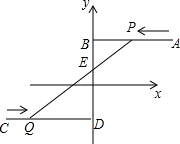 如图,在平面直角坐标系中,AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,且点A、点C的坐标分别为(8,3)和(-6,-2),两动点P、Q分别从点A和点C同时出发,分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动,设运动时间为t秒,线段PQ交BD于点E.
如图,在平面直角坐标系中,AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,且点A、点C的坐标分别为(8,3)和(-6,-2),两动点P、Q分别从点A和点C同时出发,分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动,设运动时间为t秒,线段PQ交BD于点E.(1)当E为线段BD的中点时,求线段PB的长;
(2)当P在第一象限,且△PBE为等腰三角形时,求t的值;
(3)是否存在t的值,使以PBCD为顶点的梯形的面积为15?若存在,求出t的值,并写出此时P的坐标;若不存在,说明理由.
考点:四边形综合题
专题:
分析:(1)根据相似推出BP=DQ,即可得出方程,求出方程的解即可;
(2)根据等腰求出PB=BE,DQ=DE,即可得出方程,求出方程的解即可;
(3)根据梯形的面积公式得出方程,求出方程的解即可.
(2)根据等腰求出PB=BE,DQ=DE,即可得出方程,求出方程的解即可;
(3)根据梯形的面积公式得出方程,求出方程的解即可.
解答:解:设时间是t,
(1)∵E为BD中点,
∴BE=DE,
∵AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,
∴AB∥CD,
∴△PBE∽△QDE,
∴
=
,
∴BP=DQ,
∴8-2t=6-t,
∴t=2,
∴PB=8-2t=8-2×2=4;
(2)∵AB∥x轴交y轴,
∴∠PBE=90°,
∵△PBE为等腰三角形,
∴PE=BE,
∵AB∥CD,
∴△PBE∽△QDE,
∴PB=DE=8-t,QE=DE=6-t,
∵BD=BE+DE=5,
∴(8-2t)+(6-t)=5,
∴t=3;
(3)不存在,
理由是:∵BP=8-2t,
∴S梯形=
(8-2t+6)×5=15,
解得:t=4,
即当t=4时,点P和点B重合,
所以这个梯形是不存在的,
即不存在t的值,使以PBCD为顶点的梯形的面积为15.
(1)∵E为BD中点,
∴BE=DE,

∵AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,
∴AB∥CD,
∴△PBE∽△QDE,
∴
| BP |
| DQ |
| BE |
| DE |
∴BP=DQ,
∴8-2t=6-t,
∴t=2,
∴PB=8-2t=8-2×2=4;
(2)∵AB∥x轴交y轴,
∴∠PBE=90°,
∵△PBE为等腰三角形,
∴PE=BE,
∵AB∥CD,
∴△PBE∽△QDE,
∴PB=DE=8-t,QE=DE=6-t,
∵BD=BE+DE=5,
∴(8-2t)+(6-t)=5,
∴t=3;
(3)不存在,
理由是:∵BP=8-2t,
∴S梯形=
| 1 |
| 2 |
解得:t=4,
即当t=4时,点P和点B重合,
所以这个梯形是不存在的,
即不存在t的值,使以PBCD为顶点的梯形的面积为15.
点评:本题考查了相似三角形的性质和判定,等腰三角形的判定,坐标与图形性质的应用,题目比较好,难度适中.

练习册系列答案
相关题目
 如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为
如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为 如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?
如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?