题目内容
如图，量角器上的C、D两点所表示的读数分别是80°、50°，则∠DBC的度数为考点：圆周角定理
专题：
分析：首先连接OC，OD，即可求得∠COD的度数，又由圆周角定理，即可求得∠DBC的度数．
解答：
解：连接OC，OD，
∵量角器上的C、D两点所表示的读数分别是80°、50°，
∴∠AOC=50°，∠AOD=80°，
∴∠COD=∠AOD-∠AOC=30°，
∴∠DBC=
∠COD=15°．
故答案为：15°．
解：连接OC，OD，∵量角器上的C、D两点所表示的读数分别是80°、50°，
∴∠AOC=50°，∠AOD=80°，
∴∠COD=∠AOD-∠AOC=30°，
∴∠DBC=
| 1 |
| 2 |
故答案为：15°．
点评：此题考查了圆周角定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
具备下列条件的两个三角形中，不一定全等的是（ ）
| A、有两边一角对应相等 |
| B、三边对应相等 |
| C、两角一边对应相等 |
| D、有两边对应相等的两个直角三角形 |
如图，在正方形ABCD中，AB=2，E为边BC延长线上的一点，连接DE，BF⊥DE于点F，BF与边CD相交于点G，连接EG，设CE=x，BF=y，试建立y与x的函数解析式，并写出函数的定义域．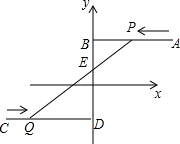
如图，在平面直角坐标系中，AB∥x轴交y轴于点B，CD∥x轴交y轴于点D，且点A、点C的坐标分别为（8，3）和（-6，-2），两动点P、Q分别从点A和点C同时出发，分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动，设运动时间为t秒，线段PQ交BD于点E．