题目内容
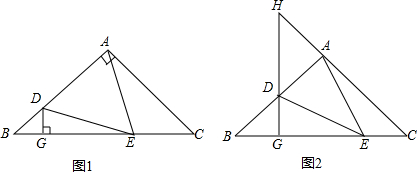
已知等腰△ABC一腰上的高与另一腰的夹角为50°,求△ABC三个内角的度数.
考点:等腰三角形的性质
专题:
分析:首先想到等腰三角形分为锐角、直角、钝角等腰三角形,当为等腰直角三角形时不可能出现题中所说情况所以舍去不计,我们可以通过画图来讨论剩余两种情况.
解答: 解:①当为锐角三角形时可以画图,
解:①当为锐角三角形时可以画图,
高与右边腰成50°夹角,由三角形内角和为180°可得,顶角为40°,底角为
(180°-40°)=70°;
②当为钝角三角形时可画图,
此时垂足落到三角形外面,因为三角形内角和为180°,
由图可以看出等腰三角形的顶角的补角为40°,三角形的顶角为140°,底角为
(180°-140°)=20°.
综上所述,△ABC三个内角的度数为40°,70°,70°或140°,20°,20°.
 解:①当为锐角三角形时可以画图,
解:①当为锐角三角形时可以画图,高与右边腰成50°夹角,由三角形内角和为180°可得,顶角为40°,底角为
| 1 |
| 2 |
②当为钝角三角形时可画图,
此时垂足落到三角形外面,因为三角形内角和为180°,
由图可以看出等腰三角形的顶角的补角为40°,三角形的顶角为140°,底角为
| 1 |
| 2 |
综上所述,△ABC三个内角的度数为40°,70°,70°或140°,20°,20°.
点评:主要考查了等腰三角形的性质及三角形内角和定理,做题时,考虑问题要全面,必要的时候可以做出模型帮助解答,进行分类讨论是正确解答本题的关键,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
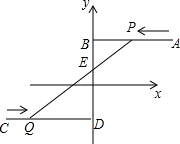 如图,在平面直角坐标系中,AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,且点A、点C的坐标分别为(8,3)和(-6,-2),两动点P、Q分别从点A和点C同时出发,分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动,设运动时间为t秒,线段PQ交BD于点E.
如图,在平面直角坐标系中,AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,且点A、点C的坐标分别为(8,3)和(-6,-2),两动点P、Q分别从点A和点C同时出发,分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动,设运动时间为t秒,线段PQ交BD于点E.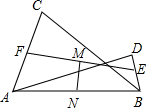 如图,AB=AD=BC,点E、F、M、N分别是BD、AC、EF、AB的中点,求证:MN⊥EF.
如图,AB=AD=BC,点E、F、M、N分别是BD、AC、EF、AB的中点,求证:MN⊥EF.