题目内容
若（a-1）2+|b+2|=0，则|a+b|= ．
考点：非负数的性质：偶次方,非负数的性质：绝对值
专题：
分析：根据非负数的性质，可求出a、b的值，然后将代数式化简再代值计算．
解答：解：∵（a-1）2+|b+2|=0，
∴a-1=0，b+2=0，
解得a=1，b=-2，
∴|a+b|=|1-2|=1，
故答案为1．
∴a-1=0，b+2=0，
解得a=1，b=-2，
∴|a+b|=|1-2|=1，
故答案为1．
点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
如图，在正方形ABCD中，AB=2，E为边BC延长线上的一点，连接DE，BF⊥DE于点F，BF与边CD相交于点G，连接EG，设CE=x，BF=y，试建立y与x的函数解析式，并写出函数的定义域．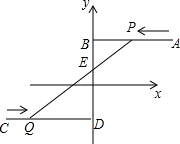
如图，在平面直角坐标系中，AB∥x轴交y轴于点B，CD∥x轴交y轴于点D，且点A、点C的坐标分别为（8，3）和（-6，-2），两动点P、Q分别从点A和点C同时出发，分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动，设运动时间为t秒，线段PQ交BD于点E．如果代数式7a3-6a2b+5a3+ma2b的值与b无关，则（ ）
| A、a=0 | B、b=0 |
| C、m=0 | D、m=6 |