题目内容
 如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?
如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?考点:含30度角的直角三角形,勾股定理
专题:
分析:作∠ACE=∠A=30°,即可得出△ACE是等腰三角形,△ECB是等边三角形,进而得出AE=CE,CE=BE=BC,所以AB=2BC.
解答: 解:AB=2BC,
解:AB=2BC,
理由:作∠ACE=∠A=30°,
∴AE=CE,
∵∠ACB=90°,若∠A=30°,
∴∠ABC=60°,
∴∠ECB=60°,
∵∠ECB=∠ABC,
∴三角形ECB是等边三角形,
∴CE=BE=BC,
∴AB=2BC.
 解:AB=2BC,
解:AB=2BC,理由:作∠ACE=∠A=30°,
∴AE=CE,
∵∠ACB=90°,若∠A=30°,
∴∠ABC=60°,
∴∠ECB=60°,
∵∠ECB=∠ABC,
∴三角形ECB是等边三角形,
∴CE=BE=BC,
∴AB=2BC.
点评:本题考查了含30°的直角三角形的边的关系,等腰三角形的判定和性质,等边三角形的判定和性质,作出辅助线构建等边三角形是关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
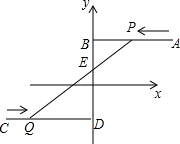 如图,在平面直角坐标系中,AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,且点A、点C的坐标分别为(8,3)和(-6,-2),两动点P、Q分别从点A和点C同时出发,分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动,设运动时间为t秒,线段PQ交BD于点E.
如图,在平面直角坐标系中,AB∥x轴交y轴于点B,CD∥x轴交y轴于点D,且点A、点C的坐标分别为(8,3)和(-6,-2),两动点P、Q分别从点A和点C同时出发,分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动,设运动时间为t秒,线段PQ交BD于点E.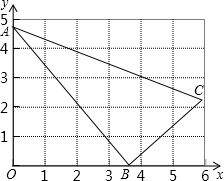 如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,
如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,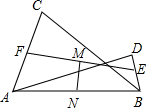 如图,AB=AD=BC,点E、F、M、N分别是BD、AC、EF、AB的中点,求证:MN⊥EF.
如图,AB=AD=BC,点E、F、M、N分别是BD、AC、EF、AB的中点,求证:MN⊥EF.